


A vibration can be represented as shown in Fig. A-1:
Vibration is motion through a transmitting medium. It can be periodic, like a wave moving up and down along the surface of the water; a sound wave moving through the air; a pendulum swaying back and forth; our ball rotating around the shaft; a planet moving in its orbit about the sun. Alternatively, it can be a sharp burst of sound or a series of non-repeating sounds, as in a musical composition, or "noise."
In Fig. A-2, there are non–repeating sharp bursts of sound.
Either way, vibration involves compression and rarefaction of the transmitting medium, or a movement back and forth. For example, the vibrating cone of a speaker creates changes in air pressure, which reach the ear and are translated into the frequencies that were recorded on the playing medium (CD, DVD, tape, LP, etc.)
Oscillation is an important concept and is the essence of vibration. The electricity that flows through our houses, for example, is alternating current at 60 cycles per second, as a direct result of a rotating coil (armature) within a magnetic field of a generator at the power plant.
The closer wave crests are to each other, the higher the frequency. A higher pitched sound will have wave crests closer together and a lower pitched sound will have wave crests further apart. Red light has a lower frequency than blue light, for instance. However, the quintessential nature of perception (or lack of it!) is dependent on the senses of the perceiver, as we've already seen with the dog whistle, or the gamma–ray counter.
Perception and communication are an interfacing of vibration, whether that is biological, electrical, or mechanical. A microphone, for example, takes pressure waves in the air and converts them into electrical signals. A speaker does just the opposite! The photoreactive surface of a CCD (charge coupled device), used in digital cameras, electronically converts light waves into pixel information that gives an accurate image of the target. These devices are all transducers. A transducer is a gadget that converts one type of energy to another, more useful kind. Microphones, speakers, batteries, galvanometers, vinyl record pickup cartridges, light emitting diodes, solar cells, antennas, photocells, thermocouples (temperature sensors), are all examples of transducers.
In our model the human senses, being composed of vibrating atoms, "sample" a universe that is itself vibrational in nature.
What is a sample? A sample is a snapshot of an event. In digital technology, a sample is the acquisition of a signal for a predetermined amount of time; in analog–to–digital converters, a snapshot of the signal is taken at every clock pulse. But this concept also applies in analog–to–analog applications, because any signal acquisition is nothing more than an interfacing between two or more vibrations. Imagine that you have a microphone and an amplifier, and begin to sing. You hear exactly what you are playing, continuously in real–time. Well, all of that sound out of your mouth must first get translated electronically. The one thing all microphones have in common is a diaphragm, which vibrates when impacted by the vibration of sound waves in the air, and which then is translated into an electronic signal by various means. How does the sound become a voltage? Through vibrational interaction! The medium of the air interacts with the medium in the microphone, whether that be a diaphragm that moves a coil or a magnet, or whatever. (There are five different technologies commonly used to accomplish this conversion, but all of them do the same thing). In every instant, the microphone "samples" the pressure waves of your voice. The sampling rate is dependent on the conversion materials used in the microphone.
Analog–to–Digital converters electronically capture an input signal (a sound wave in a recording studio, for example) and turn it into a series of numbers which can then be processed and sent back through a Digital–to–Analog converter, and then through a speaker to recreate the sound wave. That's how the music on CD's gets recorded. We'll see later on that the human body does essentially the same thing!
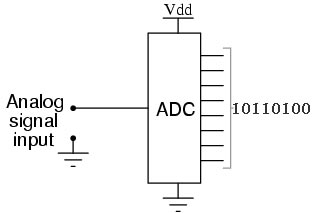
However, this is the same process as analog–to–analog conversion, because those numbers are just representations of analog voltage drops. In other words, the digital 1's and 0's in your computer or sound card are just recorded drops in voltages within the digital circuitry.
Sampling is a concept developed in digital technology, but in a vibrational universe, all perception involves sampling, whether that is accomplished electronically or biologically.
In the digital sampling of signals (used in music, in radio and TV broadcasting, and in the analysis of brainwaves and heart-beat), it turns out that a bandwidth limited signal of N cycles per second can be reconstructed without error from samples taken uniformly at a rate which is greater than 2 * N cycles per second (in analog–to–digital signal processing, you often need a higher sampling rate due to the physical limitations of sampling circuitry, but the idea holds). The maximum measurable frequency is therefore equal to half the sampling frequency, which is called the Nyquist limit. So, for example, to digitize a signal with a frequency of 1,000 cycles per second, a minimum sampling frequency of 2,000 cycles per second is required, in order to accurately recover the signal information.
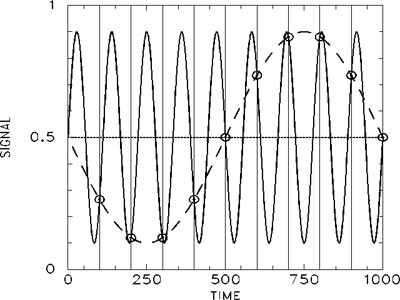
In the above diagram, the sampling rate (indicated by the vertical lines) is too low to accurately decipher the vibration indicated by the solid line, so it looks like the lower frequency dashed–line wave. If the sampling rate were reduced so that the signal is sampled once at the beginning, once in the middle, and once at the end, a straight line would result (the line in the middle) which means the vibration would be invisible. Failure to sample at a high enough rate leads to foldover, or aliasing: in the signal there are extra, unanticipated and new low frequency contributions to the sound, causing distortion and noise.
Sampling essentially quantizes a signal into discrete packets of information. One way to understand quantizing is to imagine a line drawn on a piece of paper that is 5.046875 inches long (that's 5 inches plus another 3/64th's of an inch). If you only had a ruler marked out in inches, you would measure its length as "5," but if you had one marked in eighth's of an inch, your measurement would be much closer. The smaller you can quantize the ruler, the more accurate your reading will be.
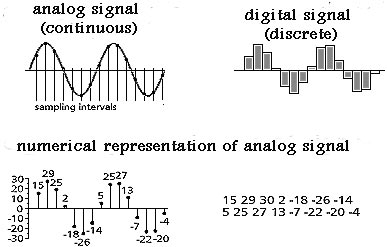
Quantization occurs in the conversion of analog signals to digital information, because the sampling circuitry needs a little time to process the signal; so the information is acquired in steps. Acquisition of the signal does not begin until a clock pulse is received; so the speed of the clock in the circuitry determines the sampling rate.
It is impossible to continuously measure or perceive anything because it takes time between the receipt of a signal, the processing of it, and re–exposure. During the time it takes for processing, you are missing out on a portion of the signal, as you can see from the above graphic. The digital signal is jerky and shows loss of information.
The input to an analog–to–digital converter is a continuous signal with an infinite number of possible states, but the digital output is a discrete function whose number of different states is determined by the resolution of the converter. Therefore, the conversion from analog to digital loses some information and introduces some distortion into the signal. The magnitude of this error is random, with values up to ±LSB, the least significant bit of the converter's resolution.
In video, undersampling leads to an incorrect impression of an object's behavior. For example, if a rotating wheel is under-sampled, its true rotational speed is underestimated, and sometimes it appears to be moving in the opposite direction. This phenomenon is observable in old movies, where a car or wagon wheel appears to be moving in the opposite direction, due to the inadequate frame rate of the recording camera. When the sampling rate is equal to the rotation, the wheel appears to be motionless!
Imagine a darkened room and a one-spoked wheel mounted on a shaft that can be rotated counter–clockwise at predetermined speeds.
The wheel is rotated 7 times, beginning at 1 revolution per minute (rpm) and continuing up to 7 rpm, and the wheel can only be seen every 10 seconds, when a light flashes. Therefore, the sampling rate, or the rate at which the wheel can be perceived, is 6 times per minute. What happens?
When the true rotational frequency is below the Nyquist limit (1 and 2 rpm), the correct frequency and direction of the rotations are observed. When the wheel rotates at the Nyquist limit (3 rpm), the wheel is seen every 180 degrees. Its rotational speed can be deduced, but its rotational direction is ambiguous. When the true rotational frequency is above the Nyquist limit, errors in observation occur. At 4 rpm, an erroneous speed of 2 rpm is estimated, and the apparent rotational direction is also wrong, clockwise instead of counter–clockwise. At 5 rpm, the rotational speed is underestimated still further (1 rpm), and the rotational direction is still incorrect:
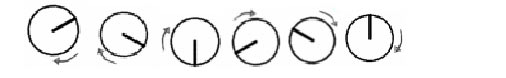
Here the wheel appears to be moving clockwise at only 1 rotation per minute, even though it is actually moving at 5 rpm counter–clockwise.
At 6 rpm, twice the Nyquist limit, the wheel is seen every 360 degrees and therefore seems to be motionless:

At 7 rpm, the apparent rotational direction is again correct, but the speed is again underestimated at only 1 rpm:
The rate at which information is gathered determines what is perceived.
In digital signal processing, signals are processed through a low–pass filter, which screens out all frequencies above the Nyquist limit. Such a signal is said to be bandwidth limited. In the physical universe, signals are usually not bandwidth limited (although a wall, for example, essentially operates as a low–pass sound filter, screening out higher frequencies); nevertheless, the perception, analysis, or interpretation of any vibration is always relative to the rate of the sampling vibration.
In audio applications, undersampling can lead to crummy sound quality (but it also has practical uses which we won't go into here); oversampling with digital filtering is used in audio to increase sound quality. Interestingly enough, oversampling (and upsampling) at rates well above the Nyquist limit actually increases sound quality, even though there is no more information in the upsampled signal than in the original!
That is to say, 44.1kHz CD data converted to a 352.8kHz datastream before digital–to–audio conversion (called 8x over-sampling) sounds better, even though both data streams have a frequency spectrum within the 20–20,000 cycles per second range of human hearing.
Upsampling has led some to theorize that human hearing is more dependent on rapid changes of sound within the time domain than on the frequency spectrum itself. It is well known that the timbre of a sound (what distinguishes the sound of a drum from that of a piano, for instance) is more dependent on the attack and decay of a sound wave (how fast it gets going and how long it takes to die out) rather than its pitch (highness or lowness). In other words, the difference in the sound of a cymbal and that of an oboe has more to do with the shape of the vibration, rather than its frequency.
Others have said that the improved sound comes from noise shaping and improved filtering of the digital data, reducing the noise floor of the signal before it gets sent out to the speakers.
Whatever the reason, it is clear that what is happening vibrationally within the human ear (and precisely how it interfaces with the brain to produce what is heard) is not fully understood. If, as we've said throughout this book, consciousness as a non–physical phenomena is introduced, then perhaps the subtle vibrational effects of analog and digital sound reproduction equipment may be accounted for.
And even though your ears can't hear infrasound, (sounds below the range of human hearing) it can affect you. Legend has it that the Nazi's used infrasound before WWII to anger and excite crowds gathered to listen to Hitler. A lot of infrasound research has been classified and it is not possible to determine what is fact and what is fiction. However, in the summer of 2003, scientists in Britain conducted an experiment to gauge the effects of infrasound, adding infrasound bass lines to the performed music. It was discovered that infrasound passages caused listeners to experience increased heart rate, feelings of anxiety, shivers on the skin, and fluttering in the stomach. In some participants, the infrasound even evoked sharp memories of emotional losses!
It seems that vibration, even if it is beyond the range of human senses, has noticeable psychological effects.
Do human beings perceive the universe in a continuous, un-interrupted manner, or can we extend the sampling concept to the human senses? Sampling is vibrational interaction, and that occurs in both digital and analog applications. Nevertheless, it is interesting to pursue the sampling idea because it turns out that the human senses operate in a sort of biologically digital fashion.
There is experimental evidence to suggest that resolution acuity of the human eye is directly linked to the spatial density of retinal neurons. The sampling theory of visual resolution states that the optical image formed on the retina of the human eye is spatially continuous, whereas the neural image is discrete. According to this theory, the same issues of undersampling, aliasing, etc. that apply in digital signal processing also apply to the human sense of sight.
The human body receives information from the outside world through receptors, which are neurons in the sense organs. Neurons, as we'll see shortly, communicate their information through a series of electrical (electro–chemical) impulses, and send this information through the nervous system and into the brain. The brain is essentially the main switching mechanism of the central nervous system; it receives (and transmits) electrical impulses. A nerve impulse is essentially an interpreted unit of information from the outside world, in the form of an electrical impulse, which makes sense to, and can be used by, the body's organs and systems.
Neurons are the primary cells of the nervous system. The nervous system transmits the information that coordinates the activity of the muscles, monitors the organs, constructs and processes input from the senses. The neuron is an example of what is called an excitable cell. An excitable cell is one that can be stimulated to generate a tiny electrical current. All cells (not just excitable cells) have a resting potential, which is an electrical charge across the plasma membrane. The interior of the cell is negative in relation to the exterior. The size of the resting potential varies, but in excitable cells it runs somewhere around -70 millivolts (mv). External stimuli can reduce the charge across the plasma membrane, which is called depolarization. If the potential is reduced to the threshold voltage (about -50 mv in mammalian neurons), what is called an action potential is generated in the cell. If depolarization at a spot on the cell reaches a threshold voltage, the reduced voltage opens up hundreds of voltage-gated sodium channels in that portion of the plasma membrane. A wave of depolarization sweeps along the cell, which is called the action potential (in neurons, the action potential is also called the nerve impulse.)
It takes between 0.001 and 0.002 seconds for human neurons to re–polarize and ready itself to transmit another impulse, which is called the refractory period. This means that the neuron can transmit 500-1000 impulses per second, which implies that although the body may be exposed to continuous (analog) signals from the environment, there is a processing delay from the time the signal is received until the neuron is ready to obtain more information. In essence, there is a sampling rate for each individual receptor.
Interestingly, the human neuron operates like a logic gate. It will respond only if the stimulus reaches a threshold level; any stimulus weaker than the threshold will produce no impulse, and any stimulus stronger than the threshold will produce an impulse. However, the impulse is always of the same strength, regardless of the strength of the stimulus. Therefore, a nerve impulse is remarkably like a "bit" of information in computer terminology. It is either "on" or "high" (a 1), or "off" or "low" (a 0). So it seems that digital devices aren't so high–tech after all, merely mimicking human biology!
The human body has billions of neurons sending and receiving information to and from the brain, and the human brain has about 100 billion neurons and 100 trillion connections (synapses) between them. There is a constant stream of electrical impulses reaching the higher cognitive functions from the senses, but this information is discrete, not continuous [It is possible to have a continuous digital output from an analog input stream; however, there is always some loss of information.] We might liken the firing time of a neuron to the "sample and hold" delay time of an ADC (analog to digital converter). In an ADC, it takes time to process the input signal and turn it into a sequence of numbers, just as it takes neurons time to send a nerve impulse and ready itself for the next transmission. Sample and hold just means that the input value must be held constant during the time that the converter turns the signal input into a bunch of numbers.
Whether a system is biological or mechanical, interpretation, conversion, or transduction is imperfect. That is why, in engineering, there is always a tradeoff between efficiency and performance. The body itself can be regarded as an engineered system (even if we often don't really understand what's going on!) so perhaps our digital analogies are not so far–fetched.
_____________________________________________
In conclusion, we can say that, in our model, physical perception must be, first and foremost, a vibrational translation or interpretation. Now we extend this concept out on the electromagnetic spectrum, far, far out, until we reach the realm of subtle energy. Subtle energy is so refined and of such a high vibration that it cannot be measured with the instruments of science. Subtle energy is the energy of thought, of life force. It is a product of consciousness itself, and it fills the universe. It is, on the subtle level of thought, an instantaneous communication medium, invisible, yet tangible. With these assumptions, it is possible to use the vibrational concept to explain non–local phenomenon such as ESP, intuition, remote viewing, and other psychic phenomena. The vibrational concept allows us to integrate the material world with the spiritual. Rather than viewing the material and the spiritual as separate, we can view them as part of the same vibrational continuum.