The Binary Circle/Sphere Pattern
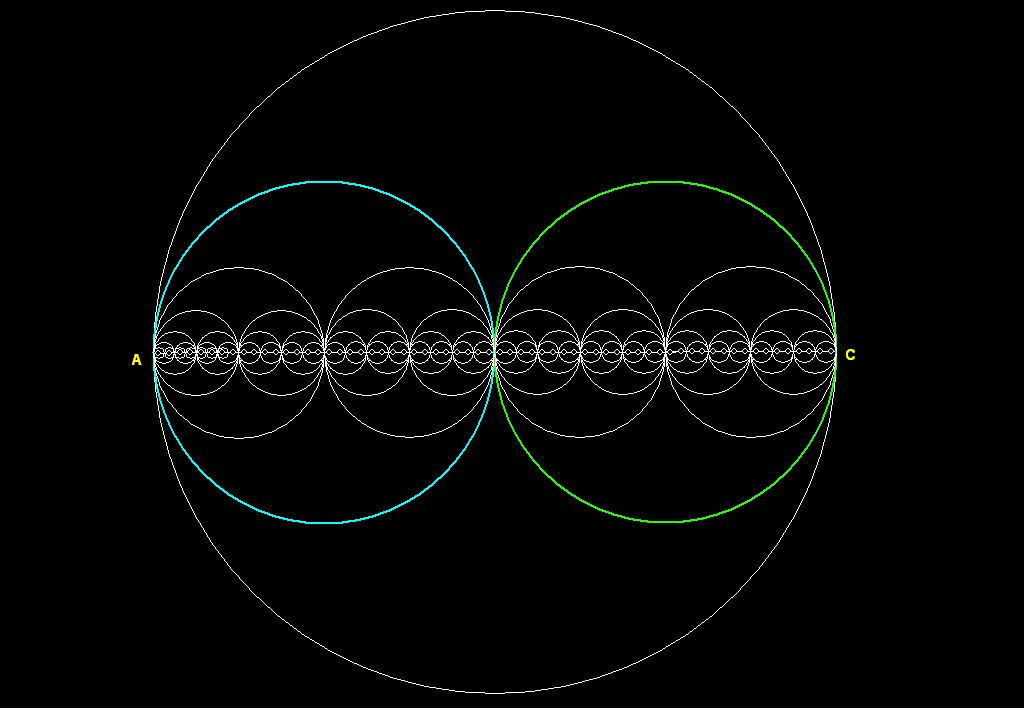
Figure 1 -- The Binary circle/sphere Pattern
The binary circle/sphere pattern is composed of 2 circles inside
a
larger circle, such that the two circles are exactly tangent to
themselves and
the larger circle.
Scale
In the above diagram we have a basic
pattern: a circle into which 2 smaller circles of exactly r/2 are
inserted.
This pattern is repeated as many times as my geometry program would
allow. As
the pattern is iterated, the circles cluster around the line AC and
become
vanishingly small.
The pattern is self-similar, meaning that it looks the same no matter
how many
times it is magnified, but it is not a fractal pattern. Its dimension
is always
2.
This pattern has some interesting
characteristics, and it got me thinking about consciousness, scales of
magnitude and observation.
If you start from A and go up on the blue circle, clockwise, 180
degrees and
come to the middle, then go down on the green circle and come to C,
then from C
go around the green circle counter-clockwise 180 back to the middle,
then down
the bottom half of the blue circle back to A, you will have made a
complete
circuit of both circles. The path traveled is exactly equal to the
circumference of the big circle. This can be seen by noting that if AC
= 2,
then r = 1 for the big circle, the circumference of the big
circle is
2*Pi. The circumference of the blue and green circles is
Pi, (2* Pi
* r/2) and so the total distance traveled around the 2 circles is 2Pi.
We can continue this pattern of traversing the circumference of the
smaller
circles indefinitely, and the total distance will always equal 2Pi.
The total number of circles upon each magnification will be 2^n, and
the
circumference around each one will be (2 * Pi) / 2^n.
For the total circumference around all of the circles, we can write
Tc = 2^n * (Pi * 2 / 2^n) = 2Pi, no matter how many times we
magnify.
Even though this is unremarkable
mathematically, it IS remarkable geometrically, because as the circles
grow
smaller and smaller, the path along the circumference of the circles
flattens
out and appears to our eyes, after only 10 iterations, to be a straight
line.
So the total distance around the circumference appears to be from A to
C in a
straight line, and back from C to A again in a straight line. To our
eyes at
'real world' magnification, it then appears that Circumference = 2*D.
By reducing the scale, we have introduced inaccuracies into our
observation of
reality.
Of course, we have microscopes and telescopes to help us resolve these questions of scale. However, even with scanning tunneling microscopes, we can observe individual atoms and even manipulate them, but we cannot yet see clearly inside an atom, so we don’t really know for sure what’s happening at the subatomic level. It’s on a scale level that is too far removed from us. Similarly for our observation of galaxies, and the universe at large. This diagram serves to illustrate that the only things we can really be sure of in the physical universe are things we can perceive directly.
Characteristics of the binary circle/sphere pattern
0) The pattern is self-similar; that is, no matter which point it is viewed from, or how deep is the magnification, it looks the same. The pattern is not a fractal, because it's dimension is always 2. (See Maths Section). The number of circles doubles after each iteration.
1) The pattern is an oscillator. As the spiral travels inward
(see Figure
2), r, the distance from the center of the spiral to any point on it,
oscillates around a point, but never reaches it.
1A) The pattern also shows curious left-and right-handed 'spirals'
which always
touch the same point every 360 degrees of revolution.
2) The pattern is a geometric representation of a simple binary search algorithm, eliminating upon each iteration exactly half of the remaining points on the line AC.
3) Notice the collapsing and expanding oscillating wave
fronts: start at A
or C. The increasing or decreasing circle radii denote an
expanding or
collapsing wave front which describe a number of behaviors:
A) Wavefronts reach greatest expansion in the middle, then
collapse to A
or C on the other side.
B) Wavefronts can expand all the way to A or C, then begin the same
expansion
process in the opposite direction.
C) Wavefronts may expand or contract at any point to any point, then
expand or
contract back in the opposite direction.
4) Decreasing circle/sphere radii sets up waveforms which
reach higher and
higher frequencies with smaller and smaller amplitudes, as the circles
get
smaller and smaller and more packed together. Even though the line AC
appears
perfectly straight, a particle traveling along it would have to wiggle
back and
forth. The diagram illustrates that a perfectly straight line cannot
exist in
nature, for it has no persistence. In other words, travel along a
perfectly
straight line would be instantaneous. It is, in effect, a wormhole or
portal
which allows perfect communication.
Anything that has persistence must have change of direction, which
generates
time. If this is true, then in order to exist at all, a Form must have
curvature.
5) Waveforms are 'paired' each with an opposite
waveform.
Observe the blue and green circles. Start at A and go up the blue
circle and
down the green circle. Then equal and opposite waveform goes back up
the green
circle and down the blue circle, exactly balancing (and zero-ing, if
the two
waves are added together) the original waveform.
Shows that every energy has its opposite, to balance it out.
6) The pattern shows what looks like magnetic lines of force
orthogonal to the
wavefronts.
(See Figure 1A just below). Note that there is really no
differentiation
between the 2 forces : they ARE the pattern.
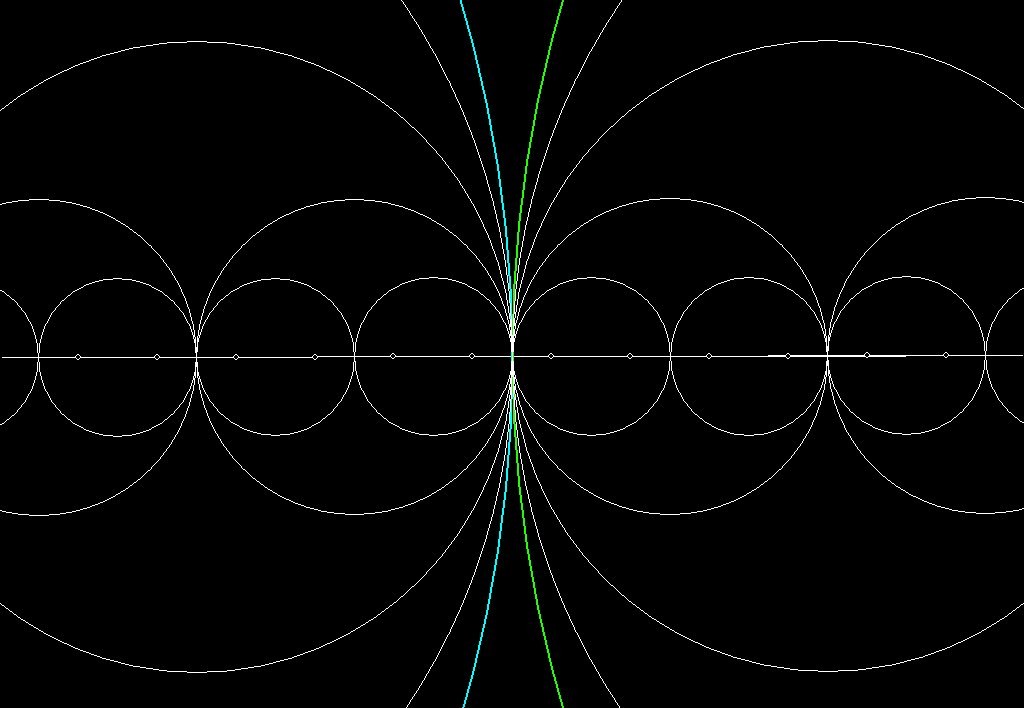
Figure 1A -- Electromagnetic energy? The waveforms from left to right
might represent
electrical energy, the magnetic lines of force orthogonal to them
represent
magnetic force, but eventually curl around and become part of the
pattern. Each
point on the pattern generates lines of force which eventually come
back to the
pattern.
So the pattern is closed, but self-generating.
Below, in Figure 2, is what a binary spiral looks like:
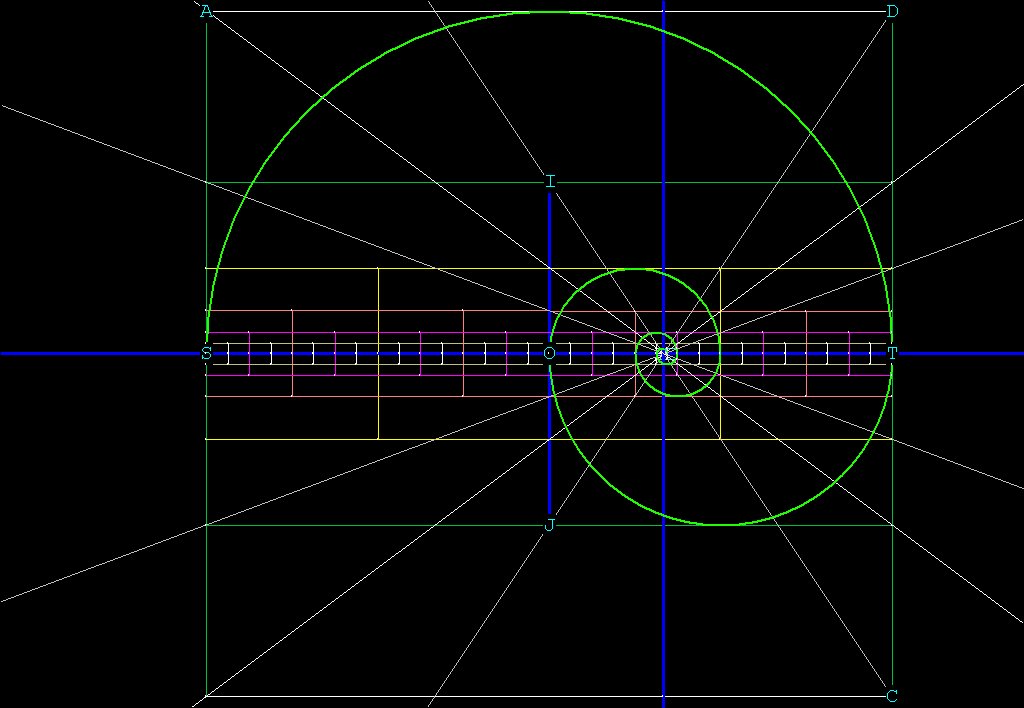
Figure 2 -- A Binary Spiral from the pattern in Figure 1. All of the
circles/spheres from Figure 1 fit inside
the
squares.
The binary spiral is generated by making squares around all of the circles in the pattern. Wherever you see a circle in Figure 1, just make a square around that circle and you will have Figure 2.
On to Maths Section
for a
mathematical description of the spiral.