The Cube

The cube has 12 sides, 8 vertices and 6 faces.
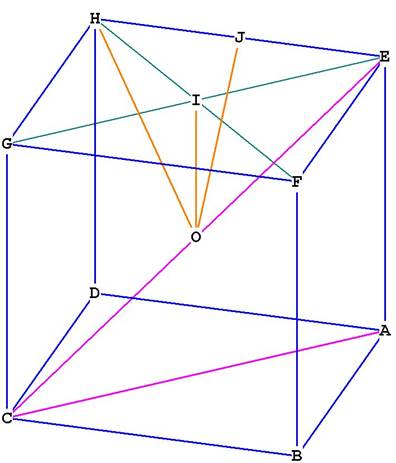
Figure 1
All of the vertices of the cube lie on the surface of the sphere. So the
diameter of the enclosing sphere is CE, or any diagonal of the cube that goes
through the centroid O.
The radius of the sphere is 1/2 that; OE, for example.
In other words, the radius is any line from O to any vertex.
The side of the cube will be referred to as s.
The volume of the cube is just s * s * s = s³
The surface area is just 6 faces * area of each face.
The area of each face is s*s = s², so the surface area = 6s².
What is the relationship between the radius of the enclosing sphere and the
side of the cube?
Look at the right triangle OIE in Figure 1. To get the radius OE in terms of
the side of the cube, notice that OI is just 1/2 BF, the side of the
cube. So OI = .
IE is 1/2 the diagonal of the face EFGH. By the theorem of
Pythagoras, GE is ,
because GH and HE are both s.
Therefore IE = .
OE = .
.
The volume of the cube in the unit sphere of radius = 1 is therefore
.
What is the central angle of the cube?
The central angle is the angle through O from any two adjacent vertices. So in
Figure 1, that would be .
We bisect HE at J to get the triangle OJE, which is right by construction.
JOE will be one-half the central angle HOE.
.
JOE =
= 35.26438968°
HOE = 2 * JOE = 70.52877936°
Central angle = 70.52877936°.
Surface angle = 90°.
Figure 2
Dihedral angle = 90°. You can see this by observing the intersection of planes BCGF and DCGH.
What is the distance from the centroid to mid-face? This is
What is the distance from the centroid to mid-edge? This is OJ.
By Pythagorean Theorem we may write
= .
OJ = .
What is the distance from the centroid to any vertex? This is OE = .
Looking at comparative distances, we have .5, .707106781, .866015404.
Cube Reference Tables
(included in the book)
