The Icosahedron
The icosahedron has 12 vertices, 20 faces and 30 sides. It is one of the most interesting and useful of all polyhedra. Buckminster Fuller based his designs of geodesic domes around the icosahedron.
The icosahedron is built around the pentagon and the golden section. At first glance this may seem absurd, since every face of the icosahedron is an equilateral triangle. It turns out, however, that the triangular faces of the icosahedron result from its pentagonal nature.
First, we’ll display 3 views of this polyhedron:
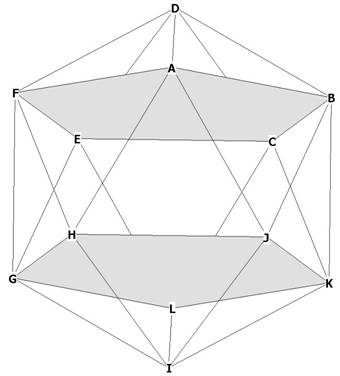
Figure 1
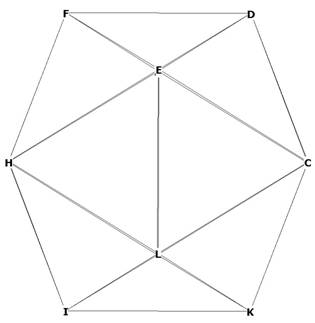
Figure 2
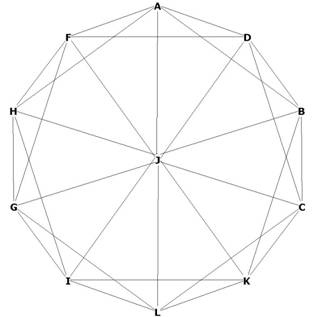
Figure 3
Figure 1 shows 2 of the internal pentagons of the icosahedron, LGFDC, and ABKIH.
Figure 2 helps to show that the icosahedron is actually an interlocking series
of pentagons. Notice the exterior pentagons at CDFHL, CEHIK, EFHIL, and CDELK.
Figure 3 shows a 2 dimensional 'shadow' of the icosa from the top down. You can
see that the outer edges form a perfect decagon, formed by the 2 pentagons CDFGL
and ABKIH.
In fact, every vertex of the icosahedron is the vertex of a pentagon.
OK, lets go through the usual analysis and then get on to the interesting stuff!
First. lets calculate the volume of the icosa.
Using the pyramid method we have 20 equilateral triangular faces which serve as
the base to a pyramid whose topmost point is the centroid of the icosa.
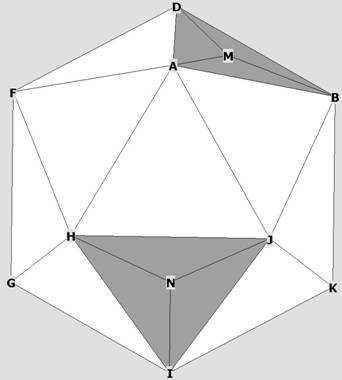
Figure 4
Some icosahedron faces with midpoints. All 20 faces will be connected to O to
form 20 pyramids.
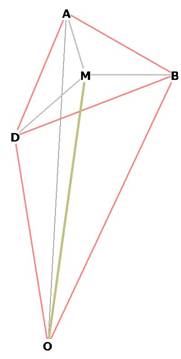
Figure 5 1 icosahedral pyramid
The volume of each pyramid is 1/3 * area of base * pyramid height.
The area of the base is the area of the equilateral triangle ADB.
The height of the pyramid is OM.
From
The Equilateral Triangle we know the area is 
All vertices of the icosahedron (as with all 5 of the regular solids) lie upon
the surface of a sphere that encloses it. The radius of the circumsphere is O to
any vertex, in this case,
r = OA = OB = OD = 1.
The height of the pyramid is h = OM.
In order to find h we need to recognize that any of the triangles OMA,
OMB, OMD are right.
This is because OM is perpendicular to the plane of triangle ABD by
construction.
AB = BD = AD = side of icosahedron = s.
Lets work with triangle OMD:
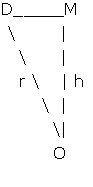
Figure 6
We know, from
The Equilateral Triangle that DM = 
In order to find h, we need to find OD = r, in terms of the side s of the
icosahedron.
To do that, we have to recognize one of the basic geometric properties of the
icosahedron.
Take a look at Figure 1. DI, BG and FK are all diameters of the enclosing sphere
around the icosahedron.
Notice rectangle BFGK and notice that BG, FK are both diagonals of it. Now
notice that both FB and GK are both diagonals of the 2 pentagonal planes marked
in gray.
We know from
Composition of the Pentagon that the diagonal of a pentagon is 
*
side of pentagon.
Therefore FB = GK = *
side of icosahedron, since each side of the pentagon is a side of the
icosahedron.
FB = *
s
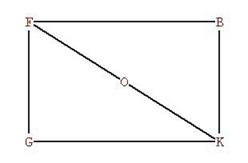
Figure 7
FK is the diameter of the enclosing sphere around the icosahedron. OF = OK is
the radius r, which we are now trying to find.
FG = BK is the side s of the icosahedron.
We have found that FB = GK = *
s .
FK =
,
r = d/2 and r = 
s.
Now we can find h, the pyramid height.
Going back to Figure 5 and Figure 6, we can write:
h² = OM² = r² - DM² =
= 
is
the height of the icosahedron pyramid.
.
So 
There are 20 pyramids, 1 for each face so
= 
= 2.181694991s³.
What is the surface area of the icosahedron?
It is just the area of 1 face * 20 faces. The area of each face is, from above,
.
So 
We have already noted the relationship between the radius of the enclosing
sphere and the side of the icosahedron:
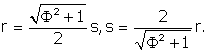r = .951056517s, s = 1.051462224r.
The side or edge of the icosahedron is slightly larger than the radius.
What is the central angle of the icosahedron?
The central angle, 
DOB,
can be seen clearly from Figure 5, and we diagram it in Figure 8 below.
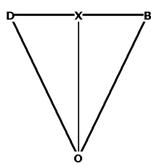
Figure 8
OD = OB = r= s.
DB is the side of the icosahedron, s.
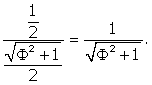
sin(XOB)
= 
XOB
= 
= 31.7174744°. DOB
= 2 * XOB.
We recognize triangle OXB as our old friend the Phi Right Triangle. From this we
know that OX / XB = .
Central angle = 63.4349488°
Surface angles = 60°
What is the dihedral angle of the icosahedron?
The dihedral angle is the angle formed by the intersection of 2 planes:
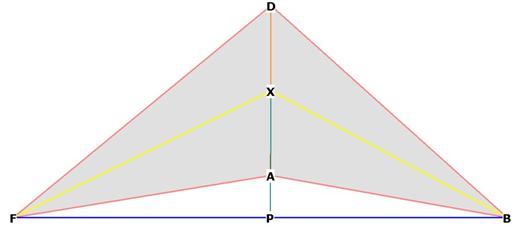
Figure 9
The intersection of the 2 faces DFA and ABD forms the dihedral angle FXB. (See
Figure 4 as well).
FX = XB we know, from
The Equilateral Triangle to be 
FB = a diagonal of one of the pentagons. This can be seen in Figure 1 or Figure
4 as the diagonal of pentagon ABCEF.
Therefore FB = *
s and PB = 
.
Triangles XPB and XPF are right by construction, so
PXB
= 1/2 FXB.
sin(PXB)
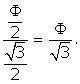
= PB / XB = 
PXB
= 
=
69.09484258°
Dihedral angle = 138.1896852°
Now lets figure out the distances from the centroid of the icosahedron to any
vertex, to any mid-face, and to any mid-side.
We already have the first two (see Figure 10). OD = OA = OB = r = 
OM = h = 
Now we need to find, for example, OX.
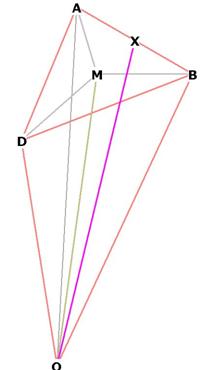
Figure 10
If we lay a 3D model of the icosahedron on one of its sides, we can see that a
line through the centroid O is perpendicular to that side. So the triangle OXB,
for example, is right.
We know AB = s, so XB = (1/2)s. OB = r, so
OX² = OB² - BX² = 
OX = 
distance from centroid to mid-face = 
=
0.755761314s.
distance from centroid to mid-side = 
=
0.809016995s.
distance from centroid to a vertex = =
0.951056517s.
Comparing distances, we have .755761314s, .809016995s, .951056517s.
Now lets get to the interesting stuff!
Going back to figure 1, we can see that the icosahedron is composed of
interlocking pentagonal 'caps.'
Look at D-ABCEF and I-GHJKL to see this more clearly. Of course , EVERY vertex
of the icosahedron is the top of a pentagonal cap, not just D and I.
Let’s analyze this cap:
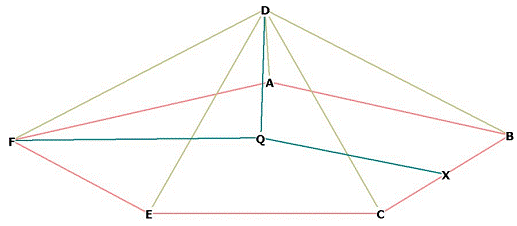
Figure 12
Triangle DQF is right, by construction. D is directly over the point Q in the
icosahedron.
How far off the plane of pentagon AFECB is D?
In other words, what is the distance DQ?
First, realize there is a circle around pentagon AFECB, even though I haven’t
draw it here. QF is the radius of that circle. We know from
Construction of the Pentagon, Part 2 that this radius
r = FQ = 
Here,
s = the side of the icosahedron.
DF is a side of the icosahedron, so DF = s. Therefore we write
DQ² = DF² - FQ² =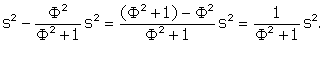 
DQ = 
Hmmm, this is looking interesting. Lets compare FQ to DQ.
FQ / DQ =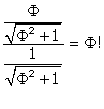 
In order to form equilateral triangles with D and the other vertices of the
pentagon, D has to be raised off the pentagonal plane AFECB by the division of
the radius of the pentagon (FQ) in Mean and Extreme Ratio.
The triangle DQF is therefore a Phi based triangle, specifically, a 
triangle.
From
The Phi Triangle we know that DFQ
= 31.71747441°.
Is this surprising? It was to me! I didn't expect something that was composed
entirely of equilateral triangles to have any relationship to .
An equilateral triangle is 
geometry, is 
geometry.
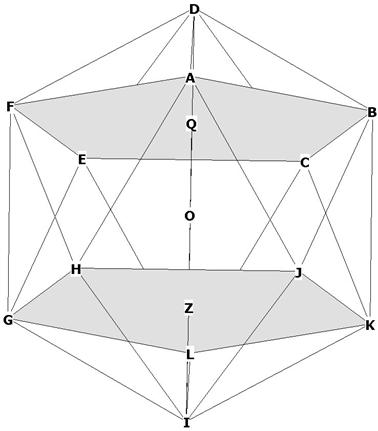
Figure 13
Here we have Figure 1 basically, with the mid-face points of the 2 pentagons
marked off as Q and Z.
We have already seen that DQ is 
with
respect to the side of the icosahedron.
That means IZ = s
as well, since IZ = DQ.
What about OQ = OZ? and QZ? How do all of these distances relate to the diameter
of the enclosing sphere, DI?
Remember that the distance DI = FK = BG, etc., is the diagonal of any of the rectangles
of which the icosa is composed. One of these rectangles
is clearly visible in Figure 12 as BFGK. We know this is a rectangle
because it is the diagonal of the pentagon ABCEF.
In fact, if you place 3 of these rectangles perpendicular to each other, the 12
corners of the 3 rectangles are the vertices of the icosahedron!
FB =
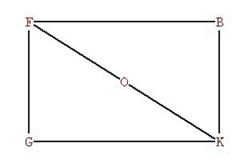
Figure 7, repeated
I have copied Figure 7 from above. FK = diameter, OF = radius of enclosing
sphere.
We know from above that
d = FK = DI = .
We have already figured out DQ = ZI. So QZ = DI - 2*DQ.
QZ =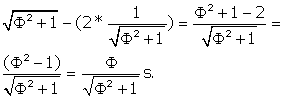 
Now,
QZ / DQ =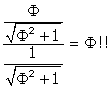 
So DZ is divided in EMR at Q (See Figure 13).
One interesting fact appears here: FQ = QZ. This means that the distance from one pentagonal plane to the other is precisely the radius of the circle that encloses the pentagon!
What is OQ?
It looks like OQ is just one-half that of QZ, or 
s.
But is it? Let’s find out.
We know OD = r = from
above.
OQ = OD - DQ =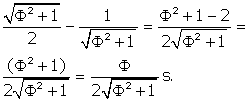 
OQ = s.
We could have gotten this more easily from the fact that
DQ = Yes,
OQ is exactly one-half QZ.
Also, OQ / DQ =
= 0.951056517
Table of Relationships
Figure 14. Central axis (diameter) relationships diameter = DI
(Available in the book).
DZ is divided in EMR by Q, IQ is divided in EMR by Z.
All of these relationships come from the pentagon!
On the outside of the icosahedron, we see equilateral triangles. But the guts
of this polyhedron comes from pentagonal relationships. The equilateral
triangles come about from the lifting of the pentagonal 'cap' vertex off the
pentagonal plane.
There is now no question that the basis for the construction of the icosahedron
is the pentagon.
Or is there?
Take a look at this view of the icosahedron:
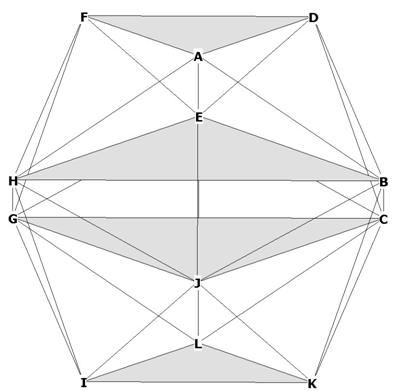
Figure 15
As you can see, the 2 pentagonal planes in the middle have magically disappeared
and become equilateral triangles! All we have done is placed the icosahedron on
one of its faces, dropping it from 30° along the x axis and 30° back along the
negative y axis.
It seems that all of our work is wrong, except:
The sides of the equilateral triangles EHB and JGC are all diagonals of
pentagons!
EH is a diagonal of pentagon FEJIH, EB is a diagonal of pentagon DEJKB, and HB
is a diagonal of pentagon AHIKB.
The equilateral triangle faces of the icosahedron are a by-product of how the
pentagons interlock. This is shown in Figure 16 below:
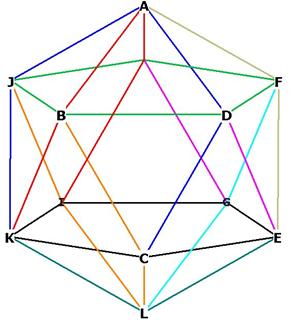
Figure 16 -- attempting to show the individual pentagons of the icosahedron
Because the pentagons are interlocking, there is duplication of colors, which
makes the individual pentagons a bit difficult to identify.
Begin with the two pentagons BDFHJ, in green, and CEGIK, in black.
Insert pentagon AJKCD, 4 of which sides are in blue.
Insert pentagon ABKIH, 4 of which sides are marked in red.
Insert pentagon BCLIJ, 4 of which sides are marked in orange.
Insert pentagon ADEGH, 2 of which sides are marked in magenta.
Insert pentagon AFECB, 2 of which sides are marked in gold.
Insert pentagon CDFGL, 2 of which sides are marked in cyan (sky blue)
The side KL in white is part of the pentagon KLGHJ.
The side LE is part of the pentagon ELIHF.
Icosaahedron Reference Tables
(included in the book)
Return to Geometry Home Page The Big Picture Home
