The
Rhombic Dodecahedron
Section 1 --- Introduction

The rhombic dodecahedron is a very interesting polyhedron. It figures
prominently in Buckminster Fuller's Synergetics.
It has 12 faces, 14 vertices, 24 sides or edges.
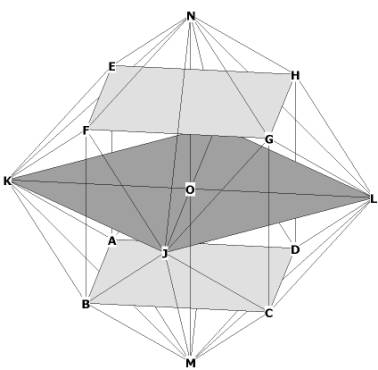
Figure 1
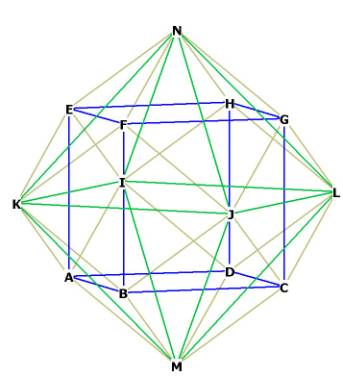
Figure 1A is Figure 1 slightly rotated, showing the edges of rhombic
dodecahedron (yellow), octahedron (green) and cube (blue).
Notice in Figures 1 and 1A that the rhombic dodecahedron is composed of
diamond faces (for example, NFJG).
The faces are called rhombuses, because they are equilateral parallelograms. In
other words, they are square-sided figures with opposite edges parallel to one
another.
The rhombic dodecahedron has 8 vertices in the middle that form a cube,
(ABCD-EFGH), and the other 6 on the outside which form an octahedron
(N-ILJK-M). It is possible to draw a sphere around the cube, and another,
larger sphere, around the octahedron.
Unlike the 5 regular solids, therefore, not all of the vertices of the rhombic
dodecahedron will touch one sphere. We will, in the course of this
analysis, find the diameter and radius of each of these spheres.
In Figure 1, I have marked the top and bottom planes of the cube in light gray,
and the square plane which serves as the base for the 2 face-bonded pyramids of
the octahedron, in dark gray.
You may perceive 3 edges of the cube in this drawing, which connect the top and
bottom planes; that is, FB,GC, HD; and also some of the edges of the
octahedron, the most visible of which are NJ, NK, NL, MK, MJ, ML. Notice
that the edges of the octahedron bisect the diamond faces of the rhombic
dodecahedron upon their long axis (for example, NK bisects the long axis of the
face NEKF at the upper left). Note also that the short axis segments (that is,
EF) are the edges of a cube.
It is important to understand that the outer vertices of the rhombic
dodecahedron form an octahedron, as this will be an important part of the
analysis.
The rhombic dodecahedron (hereinafter, referred to as r.d.) is a
semi-regular polyhedron, in that all of its edges are the same length, yet the
angles of its faces differ. Because each face is a parallelogram, there are 2
distinct angles for each face, one which is bisected by the long axis, with an
angle less than 90 degrees, the other bisected by the short axis, with an angle
greater than 90 degrees. Of course these axes do not actually appear on the
face of the polyhedron, I use them here for illustration.
In Figure 2 below, the vertices of the octahedron are the long axis vertices of
each face, in this case N and J. The cube vertices are the short axis points,
in this case, F and G. This can be more clearly seen by referring to Figure 1.
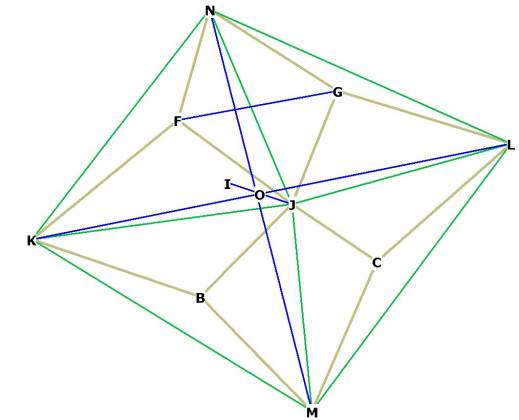
Figure 2
Figure 2 shows the general appearance of the r.d. The front 4 faces of the
octahedron can be seen clearly here in green (NKJ, NJL, KJM and JLM). Figure 2
also shows how the short axis vertices of the r.d. (as F, G, B, C) come off the
face of the octahedron.
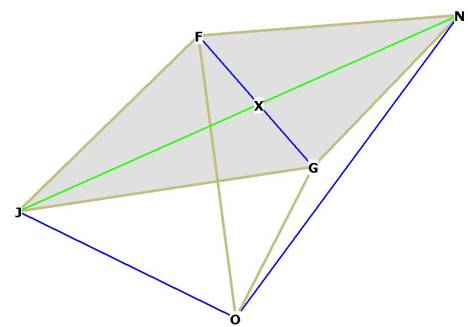
Figure 3
The sides of the rhombic dodecahedron are JFNG, one of the sides of the
octahedron is JN. ![]() JON is the central angle of the long axis of the r.d. face,
and
JON is the central angle of the long axis of the r.d. face,
and ![]() FOG is the central angle of the short axis. O is the centroid
of the r.d. and of the octahedron and cube within the r.d. When you build a 3D model of the r.d., it appears
that OF = OG = NF = FJ = JG = NG by construction; that is, the distance from
the centroid O to any of the 6 short axis vertices of the r.d. faces (the vertices
that make the cube, see Figure 1A) are equal in length to the edges of the
rhombic dodecahedron. We will prove this later on.
FOG is the central angle of the short axis. O is the centroid
of the r.d. and of the octahedron and cube within the r.d. When you build a 3D model of the r.d., it appears
that OF = OG = NF = FJ = JG = NG by construction; that is, the distance from
the centroid O to any of the 6 short axis vertices of the r.d. faces (the vertices
that make the cube, see Figure 1A) are equal in length to the edges of the
rhombic dodecahedron. We will prove this later on.
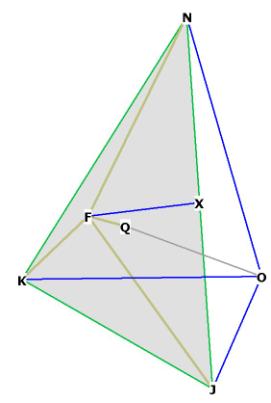
Figure 4
Figure 4 shows the point F, one of the vertices of the rhombic dodecahedron,
off one of the faces of the octahedron, NJK. The centroid of the octahedron/r.d.
is at O. Q is the center of the octagonal face NJK.
If you build a model of the rhombic dodecahedron with the Zometool you will see
at once that the sides of the r.d. come off any of the faces of the octahedron
and meet above the center of the octahedron face (for example, at F). F is also
the centroid of a tetrahedron with side length = side of the octahedron that
can be formed from the face NJK of the octahedron (see Figure 4A below). Tetrahedrons may be formed from any of the
faces of the octahedron, and connected in the fashion of Fuller’s Isotopic
Vector Matrix.
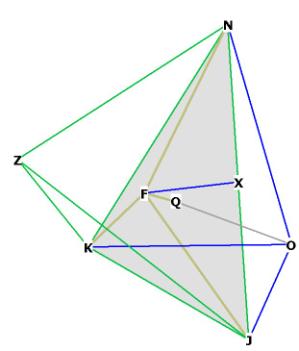
Figure 4A
QF, in Figure 4A, is the distance from the plane of the octahedron/tetrahedron
face, to the centroid of any such tetrahedron. XF is the distance from the
center of any of the diamond faces of the r.d. to a short axis vertex, in this
case, F.
OQ is the distance from the centroid to the middle of the face of the
octahedron. The centroid of the octahedron is also the centroid of the r.d.
(O), which is built around the faces of the octahedron, as shown in Figure 1.
Let's find the volume of the rhombic dodecahedron. As usual, we will use the
pyramid.
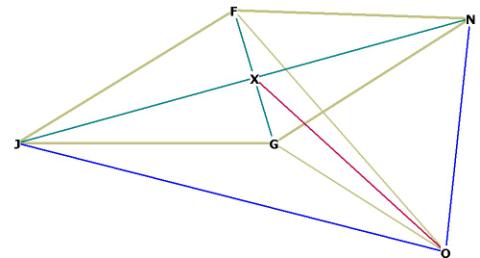
Figure 5 -- JON is 90 °
The height of any pyramid is 1/3 * area of base * height of pyramid.
We need to get the area of each diamond face.
In order to do this we need to take a rather extensive detour in which we will
derive lots of interesting information about the rhombic dodecahedron.
Section 2 -- Rhombic Dodecahedron Internals
First off, we need to know the length of the side of the rhombic
dodecahedron. In reference to what? We have an octahedron and a cube inside the
r.d. We already have the length's of each of these sides, in relation to a
sphere that encloses the octahedron and cube. The outer sphere of the r.d. is
precisely that sphere that touches all 6 vertices of the octahedron, so
we choose the edge of the octahedron as our reference point.
Recall from Octahedron that this
relationship is:
![]() .
.
Observe that the long axis NJ in Figures 1 and 2 is the side of the octahedron.
The distance ON = OJ, in blue, is the radius of the unit sphere that encloses
the octahedron.
We have remarked previously that it is possible to build a tetrahedron off of any of the faces of the octahedron that lies within the r.d. , like so:
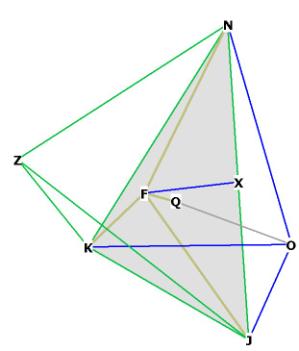
Figure 4A, repeated
Showing the tetrahedron NZKJ, which is built from the face of the octahedron
NKJ, and which has edge lengths equal to the edges of the octahedron.
The distance FX in Figure 5 is the distance from the centroid of the
tetrahedron to the mid–edge of the tetrahedron. We know from Tetrahedron that this distance = ![]() * side of the tetrahedron. Therefore, FX =
* side of the tetrahedron. Therefore, FX = ![]() * side of the octahedron.
* side of the octahedron.
Now we can find the side of the r.d. in terms of the octahedron side.

Figure 6 (Refer also to Figures 4 and 5).
NX = 1/2 the side of the octahedron, or long-axis of the r.d. face.
NF is the r.d. side.
We will refer to "os" as the side of the octahedron. "os"
is equal in length to the side of a tetrahedron whose face is congruent to the
octahedron face (See Figure 4A).
"rds" will be the r.d. side.
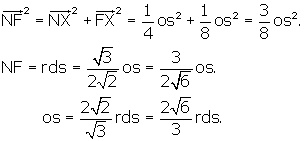
While we're at it, lets get FG, the short-axis distance on the r.d. face. FG
is visible in Figures 1,2,3 and 5. We have already established
![]() . Substituting,
. Substituting,
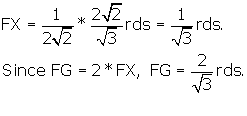
It is important to establish the distance OF = OG, the distance from the
r.d. centroid to the short axis points on the r.d. face. We have shown these in
yellow (Figure 3 and Figure 5), indicating their length is equal to the length
of the r.d. side. Is this true?
Triangle OXF is right, by construction. In order to get OF = OG, we need OX,
which also happens to be the height of the r.d. pyramid.
The height of the pyramid can be determined by inspection. From Figures 2
and 4 we see that OX goes from the centroid of the r.d. to the midpoint of the
octahedron side. But this distance is exactly 1/2 the octahedron side, as we
see clearly in Figure 7.
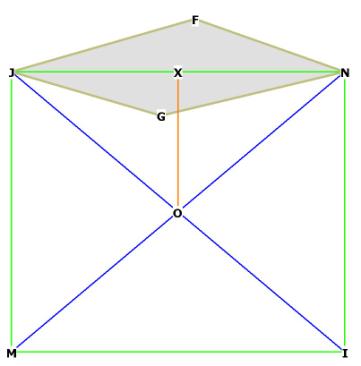
Figure 7, showing the height of the r.d. pyramid (OX) is 1/2 os, the side
of the octahedron (NI, JM).
![]() =
=![]()
Now we have the height of the r.d. pyramid in terms of the r.d. side.
![]() .
.
The triangle OXN is isosceles.
Now that we have calculated OX, it remains to prove that OF = OG. When you
build a model of the rhombic dodecahedron you can see this immediately, but
lets show it mathematically as well. We will find the result first in
terms of the side of the octahedron, then translate this with respect to the
side of the r.d.
![]()
![]() , which is precisely what we established above.
, which is precisely what we established above.
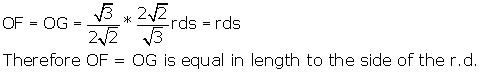
What is the relationship between OQ and FQ? From Tetrahedron and Octahedron we know that:
the distance from the centroid of the tetrahedron to the mid-face = ![]()
the distance from the centroid of the octahedron to the mid-face =
![]()
Therefore OQ = 2 * FQ, and we conclude that the face of the octahedron is twice
as far away from its centroid, as is the face of the tetrahedron from its
centroid.
We also gain the important information that triangle FOG is isosceles.
Now we can get to some important data, that is, the relationship between the
side of the r.d. and the radius of the sphere that contains the rhombic
dodecahedron. That sphere is, you recall, the sphere that surrounds and
touches the vertices of the octahedron (N-ILJK-M in Figure 1 and 1A). We will
refer to this radius as ![]() .
.
The radius of this sphere is ON = OJ in Figure 8 below. What is ON = OJ?
![]() JON is right by construction.
JON is right by construction.
Figure 8
We know that JN = side of the octahedron = os. OJ = ON =![]() , so
, so
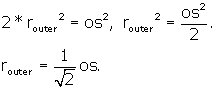
Since we found that ![]() , we substitute for os and get,
, we substitute for os and get,
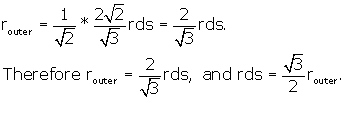
Now we have expressed the side of the r.d. in terms of the radius of the sphere
that contains the rhombic dodecahedron, realizing that this sphere touches only
the 6 outer vertices of the r.d.
Notice that FG, the short-axis distance across the face of the r.d.,
(calculated above) , also =![]() .
.
We also know from Figure 3 that the radius of the smaller sphere touching the 6
cube vertices ABCD-EFGH is equal to the side length of the r.d. We may write
rds = ![]() for this smaller
sphere.
for this smaller
sphere.
(Henceforth, we will write “r” for the radius, understanding that r = ![]() ).
).
Section 3 - The Resumption of the Volume Calculation
We were, at the end of Section 1, about to find the Volume of the rhombic dodecahedron. To do this we need to recall the height of the pyramid OX (see Figure 7), and find the area of the r.d. face.
By looking at Figure 3 we perceive that the area of the r.d. face can be
divided into 2 triangles, each one with base NJ. Both triangles are congruent
by side-side-side, and the height, ht, of each is XF = XG.
From above we know that this distance
is ![]()
NJ is the side of the octahedron, so NJ = os.
Now we have
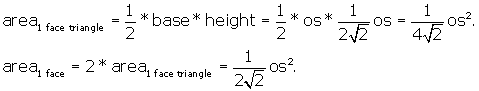
We want to get all of our data on the r.d. in terms of the r.d. itself,
for consistency. Therefore we translate the area from the side of the octahedron,
to the side of the r.d.
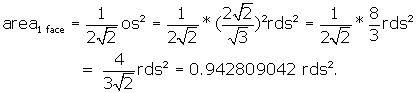
Now, finally, we have enough data to calculate the volume of 1 pyramid:
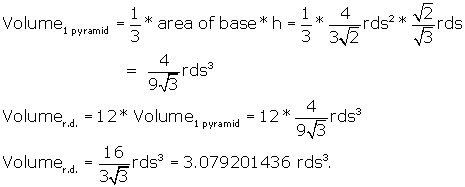
What is the surface area of the rhombic dodecahedron?
It is just 12 faces * area of 1 face = ![]()
![]()
There are 3 central angles of the rhombic dodecahedron.
In Figure 3, they would be, for example, ![]() FOG,
FOG, ![]() FON,
FON, ![]() JON.
JON.
Let's start with ![]() FOG.
FOG.
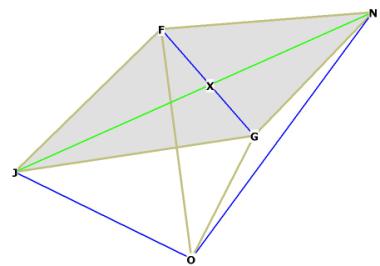
Figure 3, repeated
![]() JON is right.
JON is right. ![]() OXF,
OXF, ![]() OXG are right.
OXG are right.
To find ![]() FOG, find
FOG, find ![]() FOX. Triangle FOX is right by construction, therefore,
FOX. Triangle FOX is right by construction, therefore,
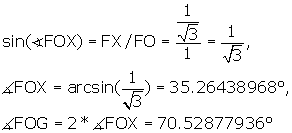
This is precisely the central angle of the cube! Understandably so, for
we already know that the two vertices F and G are two of the vertices of a
cube (see Figure 1A).
It is also the dihedral angle of the tetrahedron.
Because the triangle FOG is isosceles,
![]() OFG =
OFG =![]() OGF =
OGF = ![]() FON = (180° - 70.52877936° ) / 2, using the
property that the sum of angles of a triangle = 180° .
FON = (180° - 70.52877936° ) / 2, using the
property that the sum of angles of a triangle = 180° .
Therefore ![]() FON = 54.7356103° (and so does
FON = 54.7356103° (and so does ![]() FNO).
FNO).
From Figure 7 we can see immediately that ![]() JON is right, it being the central angle of the square JMIN.
JON is right, it being the central angle of the square JMIN. ![]() JON = 90°
JON = 90°
What are the surface angles of the diamond faces of the rhombic dodecahedron?
We know that the short-axis distance across the r.d. face,
FG in Figure 3, is ![]() .
.
We know FN = NG = the side of the r.d. = rds.
Triangle FXN is right by construction.
![]() FNX is one half the face angle FNG. FX is one- half FG.
FNX is one half the face angle FNG. FX is one- half FG.
So we can write:
![]()
![]() FNX = 35.26438968°, so
FNX = 35.26438968°, so
![]() FNG = 70.52877936°.
FNG = 70.52877936°.
![]() FNG and its counterpart
FNG and its counterpart ![]() FJG are the smaller of the two face angles of the r.d. Now
lets get
FJG are the smaller of the two face angles of the r.d. Now
lets get ![]() JFN.
JFN.
Once again we use triangle FXN and work with ![]() XFN, which is one-half the desired angle, JFN.
XFN, which is one-half the desired angle, JFN.
![]() XFN is just 90 -
XFN is just 90 - ![]() FNX, using the property that the sum of all angles in a
triangle is 180°.
FNX, using the property that the sum of all angles in a
triangle is 180°.
![]() XFN = 54.73561032°, so
XFN = 54.73561032°, so
![]() JFN = 109.4712206°.
JFN = 109.4712206°.
This angle, 109.4712206°, is the central angle of the tetrahedron and the
dihedral angle of the octahedron. It also is the angle you see when you stand
the rhombic dodecahedron on one of its 8 octahedral vertices and look down from
above at two intersecting r.d. sides. This polyhedron an all-space filler,
meaning that it can be joined with itself, like the cube, to fill any volume
without any space left over.
What is the dihedral angle of the rhombic dodecahedron? To see this
calculation, click on
Rhombic Dodecahedron Dihedral Angle
If you examine the r.d. from the inside out with the zometool, you will see
it is composed internally of the same rhombi.
To identify these internal rhombuses, lay the rhombic dodecahedron flat on one
of its faces. Find 3 r.d. points and the centroid to see the rhombus:
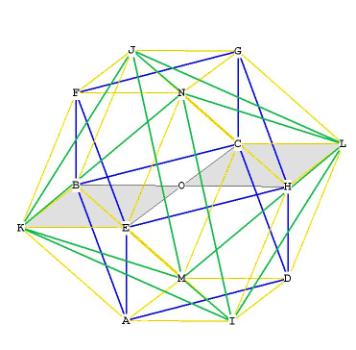
Figure 9 – two of the 12 internal rhombi of the rhombic dodecahedron. O is the
centroid.
There are 12 internal rhombi, and 12 external rhombi, each of them identical.
Note that there is another angle on the exterior of the rhombic
dodecahedron, and that is the angle that one face plane makes with another face
plane as it goes over top of the octahedron within the r.d. This angle is 90°.
This can be seen by looking at the long axis diagonals of the octahedron
through the rhombi, and following the faces that form around the side of the
octahedron. In Figure 1, this can be seen with the faces NFJG and JBMC. Notice
the lines NJ and JM, which are part of the octahedral square, and which bisect
the faces along their long axis. ![]() NJM is a right angle, as is
NJM is a right angle, as is ![]() NLM and
NLM and ![]() NKM. Observe also
NKM. Observe also ![]() KNL. Again, this property helps the rhombic dodecahedron to
be an all-space filler.
KNL. Again, this property helps the rhombic dodecahedron to
be an all-space filler.
Now lets complete the analysis of the rhombic dodecahedron by finding or
collecting the distances from the centroid to a short-axis vertex, a long-axis
vertex, mid-edge and mid-face. We already have all of this information, except
for the distance from the centroid to a mid-edge:
distance from centroid to long-axis r.d. vertex (vertex of the octahedron) = ![]() .
.
distance from centroid to short-axis r.d. vertex (vertex of the cube)
= rds.
distance from centroid to r.d. mid-face (mid-point of octahedron side)
= ![]()
To find centroid to r.d. mid-edge requires a little work:
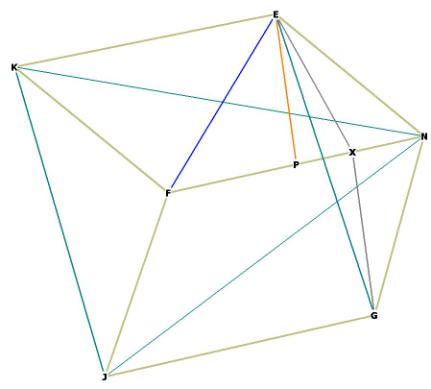
Figure 9 -- showing centroid to mid-edge distance EP.
We have already remarked upon one of the properties of the r.d., that it is
composed of 12 internal rhombi identical to the external faces. Those rhombi
are divided in half (here, at EF) by the same distance as from the centroid to
any of the vertices of the octahedron contained within the r.d. Therefore the
r.d. is composed of 24 exterior congruent triangles (here, ![]() EFN and
EFN and ![]() EKF), and 24 interior congruent triangles congruent to the
exterior ones!
EKF), and 24 interior congruent triangles congruent to the
exterior ones!
So triangle EFN may substitute for any triangle in the interior of the r.d.,
and more to the point, the vertex E or F may substitute for the centroid of the
r.d., at O. In order to see this clearly, you have to build a 3D model of the
rhombic dodecahedron, and I encourage you to do this.
From Rhombic Dodecahedron Dihedral Angle, we
know that ![]()
We know that ![]() EXN is right by construction, and that EN = rds. We also know
that P is at mid-edge on FN, the side of the r.d., therefore NP = 1/2 rds.
EXN is right by construction, and that EN = rds. We also know
that P is at mid-edge on FN, the side of the r.d., therefore NP = 1/2 rds.
We can find XN, and so XP, by writing XP = NP - XN.
We need to find XN.
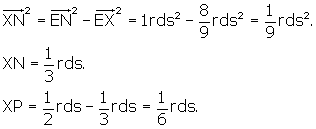
Now we can find EP, the distance from centroid to mid-edge.
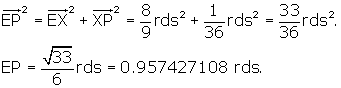
The Dihedral Angle of the Rhombic Dodecahedron
When calculating dihedral angles, it is vital to ensure that the angle
chosen is an accurate representation of the intersection of the 2 planes. In
the rhombic dodecahedron (r.d.), this is a little tricky.
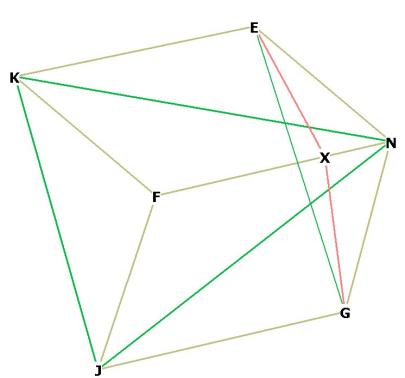
Figure 1 -- The r.d. dihedral angle
The dihedral angle of the r.d. is the angle EXG. This angle is a
geometrically accurate description of the intersection of any 2 planes of
the r.d., in this case, the 2 planes KENF and JGNF. The lines EX and GX are
constructed such that ![]() NXG and
NXG and ![]() NXE are right.
NXE are right. ![]() EXG is a
"roof" over the 2 planes which exactly describes the dihedral angle.
EXG is a
"roof" over the 2 planes which exactly describes the dihedral angle.
We will be working with triangle EXG .
It's easier to see this if you construct a model of the rhombic dodecahedron,
and lay it on one of its edges.
I have shown EG in green, indicating it is equal to the side of the octahedron
(referred to as os). We have to show this.
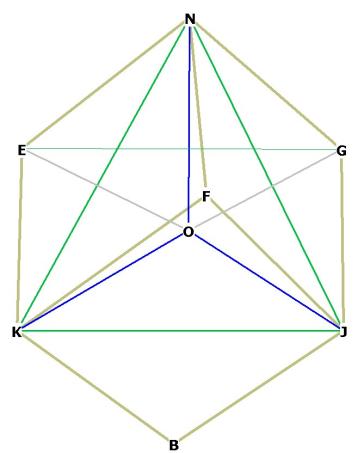
Figure 2 O is the centroid. NKJ is one of the faces of the octahedron. ON, OK and OJ are radii of the outer sphere that touch the 6 octahedral vertices. OE and OG touch the short axis vertices of the r.d.
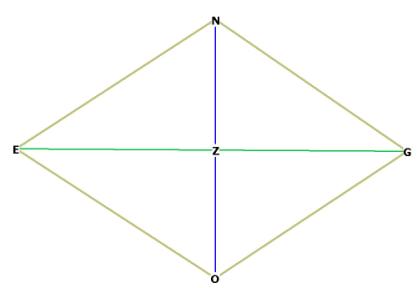
Figure 3 -- another view showing how EG is found. NEOG is one of 12 internal rhombi of the rhombic dodecahedron.
OE and OG are the sides of the rhombic dodecahedron, or rds. We have
previously shown that the triangles OEN and OGN are isosceles and congruent
(the vertices may have different names, but the triangles are the same!) NZE is
right by construction
To obtain EG, simply re-do the calculation we did previously,
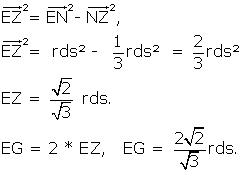
which has been obtained previously as os.
Therefore EG is identical in length to the side of the octahedron.
This internal rhombus, NEOG, is identical to the rhombus of the r.d. face.
The r.d. is composed, internally and externally, of identical rhombi, which
gives it the quality of an all-space filler.
We have established EG as the side of the octahedron. Now it remains to
determine GX and XB.
Look at Figure 1 again. The triangle ENX is right by construction, and we know
the angle ENX, it being the long-axis angle of the r.d. face, as ![]() , or 70.52877936 degrees.
, or 70.52877936 degrees.
We also know EN = side of the r.d, or rds.
So we write sin(![]() ENX) = EX / EN = EX / rds.
ENX) = EX / EN = EX / rds.
EX = rds * sin(70.52877936) = 0.942809042 * rds = ![]() rds.
rds.
(Note: EX = ![]() os).
os).
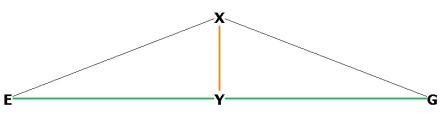
Figure 4 -- showing the dihedral angle in simplified fashion
Now, EX and EY are known. We need to get ![]() EXY.
EXY.
We know EG is the side of the octahedron, or os, and it is ![]() rds and so EY is
rds and so EY is ![]() that.
that.
sin (![]() EXY) = EY / EX =
EXY) = EY / EX = 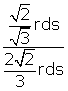 =
= ![]() .
.
![]() EXY =
EXY = ![]() = 60°
= 60°
Therefore ![]() EXG = 2 *
EXG = 2 * ![]() EXY = 120°
EXY = 120°
Dihedral angle of the rhombic dodecahedron = 120°
Rhombic Dodecahedron Reference Charts
(included in the book)
Return to Geometry
Home Page The Big Picture Home
