3 Dimensional Geometry --from a metaphysical point of view
We will proceed in 3 dimensions as we did in two
dimensions.
We are Pure Awareness, with the ability to create through thought.
Nothing exists. There is no space, no time, no somethingnesses. We
think
a thought as before, thus creating a POINT and a space between us and
it.
We take our point and move it about our self until it comes back to the
same spot, thus creating a circle.
Figure 1
Then we get the bright idea to 'flip' the circle over
ourselves.
When
we do this we are astonished to have created a uniformly symmetrical
cocoon
of energy that completely surrounds us. We call it a sphere. The sphere
is the basic 3 dimensional shape in this universe (apologies to
Buckminster
Fuller!)

Figure 2
This excellent animation (1) was taken from the U.S. Naval
Observatory (2).
Even though it is an animation of the phases of the moon, it serves
to show how a circle rotated about it's center 180 degrees will form a
sphere.
Now we can go to any POINT (call it A) on the surface of
the sphere
and repeat the process.
When we do this something very important happens: the 2 spheres
intersect
each other. like so:
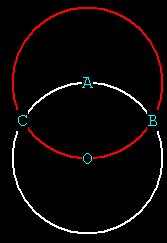
Figure 3
We have created 2 intersecting points on the outside of the original
sphere, at the outer edges of the sphere with center at A Lets call
these
POINTS B and C. If this were a 3_D pic you could see more clearly
the intersections of the 2 spheres. It forms a football shape called a
vesica. Something interesting happens inside this vesica: the mingling
of the energies of both spheres creates an excited state of energy. The
convex shape of the vesica has an effect similar to that of a
magnifying
glass placed close to a source of light: it focuses it, makes it more
intense.
The POINTS B and C are very important: they make possible the
containment
of the energy within the field. Whereas a lens is just circular but
still
focuses light, the vesica with its terminating POINTS B and C
helps
not only to focus the energy with the vesica to an excited state,
resulting
in the creation of a more powerful energy than in the original two
spheres,
but it also creates points of transmission and enhanced consciousness.
Remember POINTS are conscious! The POINTS B and C are where the entire
energy 'package' is intensely focused. The vesica then is an enhanced
or
excited energy state delegated by the 2 terminating POINTS. The vesica
is, as it were, a field of consciousness!
These 2 POINTS are like singularities. They have the property
of sending or receiving a focused beam of energy.
Also, the 2 points act somewhat like the 2 ends of a standing wave:
If you take a wire and tie it down at both ends, then give it a rap, it
will begin to vibrate and look like this:
[pic of standing wave 1 octave].
We will see later on how the intersection of spheres forms vesicas
of smaller and larger dimensions, resulting in an almost infinite
variety
of vibrations of energy.
In other words, the energy within the vesica is
focused by the
2 POINTS B and C, resulting in the creation of a more powerful
energy
than the energy contained within the 2 spheres originally. This is an
example
of synergy, where the interaction of 2 or more elements results in
something
which is greater than the sum of its parts. The vesica is a transmitter
of energy, but it can also be a receiver of energy. It's no coincidence
that the eye socket of the human being is shaped like a vesica.
OK.
Going to B and in turn C, creating spheres as we go along, we find
D and E.
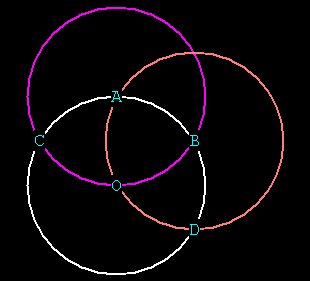
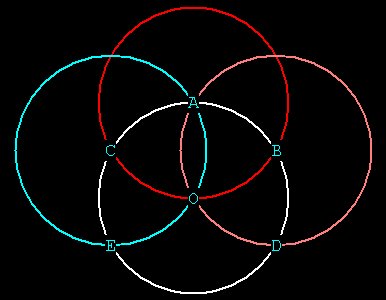
Figure 4
If we continue around the the original circle and draw spheres at D
and E, we find one more point F.
Then drawing a circle at F we complete the circuit:
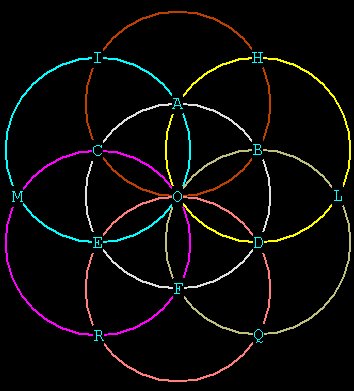
Figure 5
Just as we found in 2 dimensions, we have created a
hexagon!
It
is even cooler in 3 dimensions because we can see that the
intersections
of the spheres form egg-shaped enclosures called vesica's.
We can now go out to one of the 6 spheres we created on top of the
original sphere at A, and do the same thing. In fact, we can continue
this
process indefinitely. Apparently the ancients knew about this
pattern
because it appears (from the pink circle inward) in temples from Egypt
to Ireland (3).
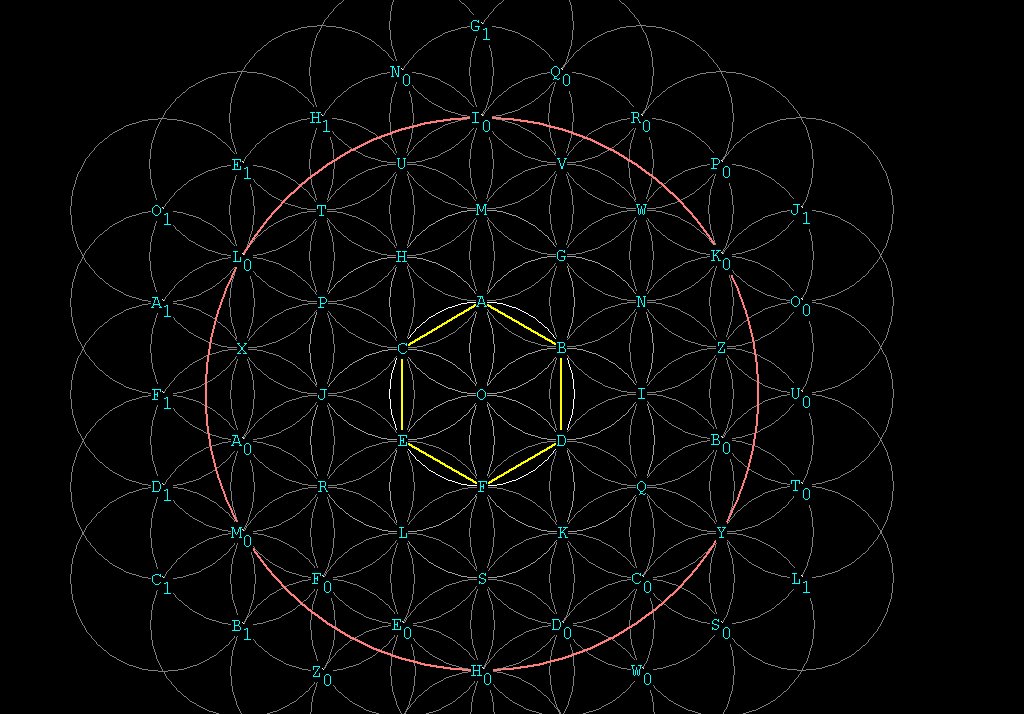
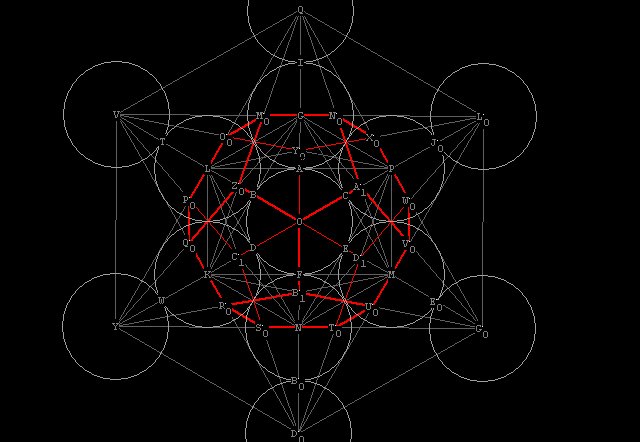
Figure 6 -- the intersecting sphere pattern
Notice that there are 2 sizes of vesicas in the pattern above:
the smaller (e.g. from O to F)
and the larger (e.g. from O to C to A to B). The ratio between the
long axis (CB)
and the short axis (OA) is \/¯3. The ratio between
the long and short axis of the smaller vesica's is
2 + \/¯3. (See Maths
Page ).
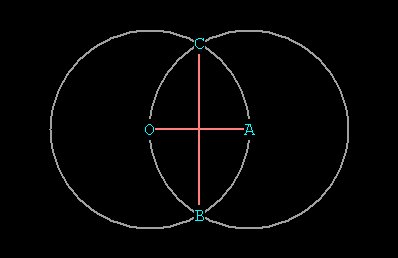
Figure 7 -- a vesica, the intersection of 2 spheres
Notice the sine waves that are interwoven throughout the
structure.
These sine waves, combined with the nodes at the ends, form standing
waves.
As you can see there are wave patterns for both the smaller and
larger
arcs. Of course all of this is in 3 dimensions really, so the wave
patterns
go all over the energetic "surfaces" of each of the vesicas. These are
the paths for energy interconnection. Remember we said earlier (2
Dimensional
geometry basics) that the curved line represents
something-that-can-be-perceived,
since there is constant change of direction. Within this structure
there
are an infinite number of possible paths, which mean an infinite number
of direction changes. This gives the structure its persistence and
creates
time, since the consciousness within it is constantly exploring itself.
Of course we have drawn all of the spheres with a radius of length
OA. Now that we know how to do this, we can re-do the entire thing with
spheres, say, of radius 1/2 OA. And 1/3 OA. And 2 * OA, etc. to
infinity,.
superimposing all of the new patterns of intersecting circles over each
other. Imagine all of the intersections, all of the vesicas formed, all
the excited and activated energies within each of the infinite number
of
smaller and larger vesicas that will form! The entire structure is
totally
dynamic and self-sustaining, because each of the POINTS which comprise
all of the nodes are conscious, and the vesicas activate, transfer and
reactivate the energy of consciousness within the entire structure. All
of the energy is continually hitting nodes, so the POINTS can
dampen
down the energy level or increase it. So the structure is self
regulating.
The frequencies and amplitudes of all of the standing waves vary with
the radius of each of the spheres. So there can be an infinite variety
of wave frequencies and wavelengths within the structure.
This pattern of intersecting spheres may seem physically
impossible
until you remember that physics has shown there are no continuous
surfaces.
In the standard scientific model of the atom (which I believe is a
metaphor)
all atoms are 99.9% space: a nucleus surrounded by a probability cloud
of electrons. The solar system is a good example of an atom: if you
calculate
the volume of space of the solar system and compare it with the volume
of space occupied by the masses within it (sun and planets), the masses
occupy a trivial portion of the overall volume. And then consider that
these masses are not 'solid' but are themselves composed of molecules
and
atoms which are themselves 99.9% space. So what appears as
'solid'
matter to us isn't really solid!
If you remove every sphere with a center on the surface another sphere,
you have a pattern of tangent, or 'closest packed' spheres. This
pattern
of tangent spheres is Buckminster Fuller's Isotropic Vector Matrix.
Buckminster Fuller said that there are no straight lines in nature
and he was right. He claimed that all lines which appear straight are
in
fact curved lines with a very large radius (505.02,
555.21).
Fuller claimed these lines were discontinuous because of quanta
energy
packing, (thus explaining the wave/particle duality). He further
claimed that the basic unit, or quanta, of energy in the universe is a
tetrahedron, and that all straight lines are actually tetrahedrons with
one of the vertices pulled away from the other three. This may very
well
be, but if so, these tetrahedrons are curved, or spherical
tetrahedrons.
Whether the curved lines in the intersecting sphere structure are
discontinuous
or not, they are still curved!
The pattern as it is drawn here only shows spheres in the
xy plane,
or across the screen as you are looking at it. In 3D there are spheres
stacked above and below the drawing surface. In 3 dimensions the
vesicas
look like footballs going into and out of the drawing surface. Below is
a crude representation of what one of the large vesicas might look like
in 3D:

Figure 7B -- the blue 'football' (vesica) comes out of the page and
down into the page in 3 dimensions.
Figure 7C: If you imagine the spheres coming out of the
page and
going
into the page, you will have the pattern in 3D. Notice that the spheres
in the xy plane (on the computer screen) are offset 60 degrees from
each
other, relative to the origin, O.
In 3 dimensions, of course, the pattern comes up out of the screen
and down into the screen.
In 3D, the spheres are also constructed so that the angles between
the origin O and the spheres on the positive and negative z axis (up
and
out, down and out of the computer screen) are also 60 degrees.
Figure 7c shows Fuller's 3D Vector Equilibrium (Cubeoctahedron). The
top of the cubeoctahedron is shown in bright yellow, the bottom half in
lighter yellow.
You may be able to visualize this if you imagine 6 spheres coming
outward toward you, with centers at F3, H3, J3, L3, K3, and I3,
(sitting
'above' the pattern): 
Figure 7C -- the cubeoctahedron in 3D
Another interesting thing about the pattern is that in its
2
dimensional
representation in Figure 6, it can be considered a diagram for a series
of intersecting 3 dimensional torii (see also Figure 7D below). For
example,
in Figure 6, the circle at A and the circle at F are tangent at
O.
But if one of the circles rotates 180 degrees around a line JOI,
it becomes the other circle and forms a horn torus.
Similarly, because the pattern is entirely symmetric, any 2 non-tangent
circles may rotate to form a ring torus ( a doughnut, basically).
And any 2 intersecting circles (forming any of the large or small
vesicas)
may rotate around the axis formed by the endpoints of the vesicas to
form
a
spindle torus.
Because rotating torii form vortexes, this pattern can be seen to be
able to funnel energy from just about anywhere to just about anywhere!
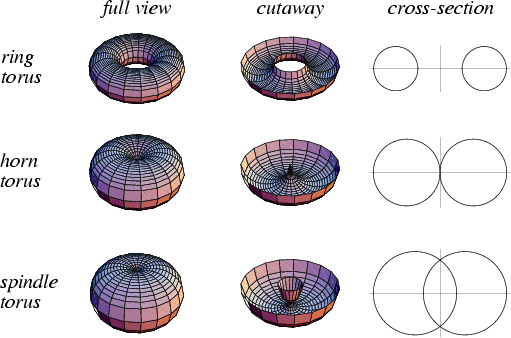 (5)
(5)
Figure 7D -- the three standard torii, showing cross-sections. Note
that these cross-section circles exactly match the circles in the
intersevcting
circle/sphere pattern. The 3 dimensional vesicas can clearly be seen in
the spindle torus.
A ring torus is formed when a circle rotates around an axis. If the
rotation is clockwise, energy will come into the torus at one end,
forming a vortex, and exit through the other end. This will form a
vortex with energy flowing in one direction only. But if we postulate
another, counter-rotating circle superposed over the original, we get
energy flowing in exacrty the opposite direction, meeting at the center
and forming a stable mass. Perhaps this is how matter and energy is
formed in the universe! When a torus rotates, then, energy is flowing
in and out of the torus, rotating clockwise and anti clockwise, forming
a spherical, toroidal field.
If one postulates the intersecting sphere pattern filling the entire
universe, one can see that it is possible to form super-galaxies as
well as the tiniest subatomic particles. In this formulation, all
matter and energy is vibrational, and all matter and energy is
surrounded by a spherical-toroidal field of energy formed by counter
rotating energy formed from the pattern. So all things in the universe
are alive, for they are all surrounded by a nurturing field of energy
which creates the object, and which is, at the same time, "breathing"
in and ejecting (refreshing itself) from the universal medium!
Here is a crude diagram:

We will show in the next diagram how the 5 basic regular
polyhedra
(including
the tetrahedron) can be formed within the structure:
Because the pattern of intersecting spheres is inherently
hexagonal
(triangular) and based upon the \/¯3, it is not immediately
obvious
how we can get to structures like the pentagon, which involve the
\/¯5.
The \/¯2 (and thus the square and the cube) can be derived easily
from this pattern, because it just involves the bisection of 2 of
the central angles within the hexagon pattern, as we saw earlier:
(e.g., bisecting <COF and <BOD is trivial because of the nodes J
and I, see Figure 6).
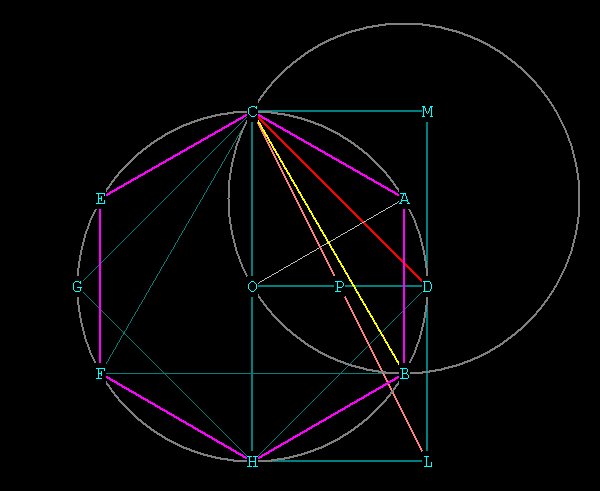
Figure 8 -- roots
The \/¯2 is CD in red. It's just the side of the
square
CDHG. Notice that it easily fits into the pattern because the points G
and D are simple bisections of the line CH which comes from the hexagon
(in purple).
The \/¯3 is line CB, which is the long axis of the vesica COBA,
which we demonstrated above. It also fits easily into the pattern
because
it's just 2 vertices (C and B) of the hexagon.
But the \/¯5 (CL in orange) is different. The ending point for
it is somewhere ugly. In order to get it we need the double
square
CMDO and ODLH. CL is the hypotenuse of the triangle CHL. CH is 2,
because
the radius CO =OH = 1. and HL = OD = radius = 1, so we have a
1,2,\/¯5
triangle.
The golden ratio is itself built upon the \/¯5. Life
is built
upon
the \/¯5! If you look into the structure of DNA you find the
pentagonally-shaped
deoxyribose-sugar component of the nucleotide, the basic building block
of DNA:
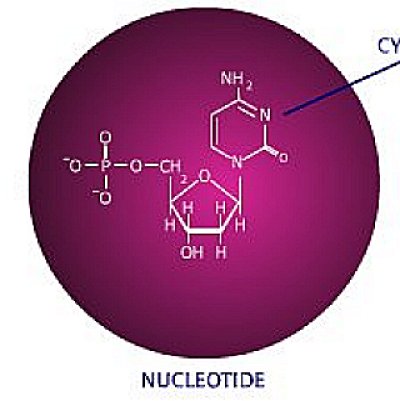 (4)
(4)
Figure 9 - the nucleotide
As you can see from the above pic, the phosphate group (to the
left)
is square, and the nitrogenous base is hexagonally shaped.
The nucleotide combines \/¯2 geometry (the
square phosphate group), \/¯3 geometry (the
hexagonally shaped nitrogenous base) and \/¯5
geometry (the pentagonally shaped deoxyribose-sugar),
but the basis for its structure is the centrally located deoxyribose-sugar!
Life, at least human, plant, and animal life, is an
approximation!
Just as the golden mean must be approximated by nature in the Fibonacci sequence, so to must DNA itself be
a 'stretch' in the fabric of
existence.
It is the division in extreme and mean ratio which can never be
precisely
nailed down which gives life its quality of tension and dynamic growth.
You can see from the pattern of spheres how easy it is to get growth
triangularly, cubicly, hexagonally -- snowflakes, minerals, crystals,
etc.
all grow effortlessly on this pattern.
(For a detailed description, with pics, of crystal lattice
structures,
and thus life forms based upon \/¯2 and \/¯3 geometry, see
the
fantastic web site at
<http://www.kings.edu/~chemlab/vrml/index.html>.)
But pentagonally-based life as we know it must think real
hard and
'reach'
for an uattainable goal -- the perfect division into mean and extreme
ratio in order to form the pentagon. Pentagonal designs do not 'fit in'
precisely to the structure of existence!
I believe that this is/was done on purpose. It is what gives life it's
dynamic and yes, its quality of tension-- the constant search for
perfection.
That is what creativity is.
In other words, pentagonally-based life has an inherent element of
tension built into it, unlike other life forms which effortlessly
replicate
along the easy-to-find nodes of the intersecting spheres.
The fact that tension generates energy is found in tensegrity.
Tensegrity
structures generate energy internally and are immediately responsive to
changing conditions. (See The Geometry
of Harmony ).
Buckminster Fuller found that many polyhedra can be easily
found
within
his Isotropic Vector Matrix, but the icosahedron and especially the
dodecahedron
caused difficulties. Fuller used the 'jitterbug' to describe how the
cube-octahedron
transformed into the icosahedron (which although basically triangular
is
pentagonal as well) but never could incorporate the
dodecahedron,
which is composed of 12 pentagons. This is because the IVM is
incomplete
in the sense that the pentagon is a wild card and will not fit
precisely
into it. When we get to the dodecahedron we will see how it is
formed
'ugly' within the structure of intersecting spheres.
Why do we say it is impossible to perfectly construct
pentagonally-based forms?
From A Geometric Construction of the
Golden Mean Spiral we see how easy it is to divide any line segment
in Phi ratio. Therefore, it should be possible to build perfectly
harmonious life forms based upon the pentagon! (I am reprinting this
sequence for clarity):
Take any line AB:

Now, bisect the line AB and transfer that distance to BC:

BC is one-half AB, and is perpendicular to AB.
Connect A to C with the straight-edge. Pin the compass at C
and place
the marking leg at B. Draw an arc to intersect AC at D. Now CD =
CB.
Now pin the compass at A and place the marking leg at D. Draw an arc
to intersect the line AB at E. Now AE = AD.
The line AB has now been divided in Mean and Extreme Ratio at E:
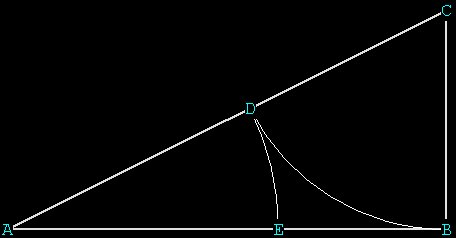
The difficulty arises when we try to precisely find the
point E! We can never quite get a perfect location. We're always off
just a little bit in practice from our theory. Perhaps this is the
reason Nature seems to prefer working in whole number increments.
OK. Now we will use the intersecting sphere pattern to
produce (as
best
as I can here) the 5 regular polyhedra -- tetrahedron, octahedron,
cube,
dodecahedron, icosahedron.
We will take out some of the spheres for clarity, otherwise the drawing
would be too busy.
First, the tetrahedron and the cube . Here we show 2
tetrahedrons
contained within a cube:
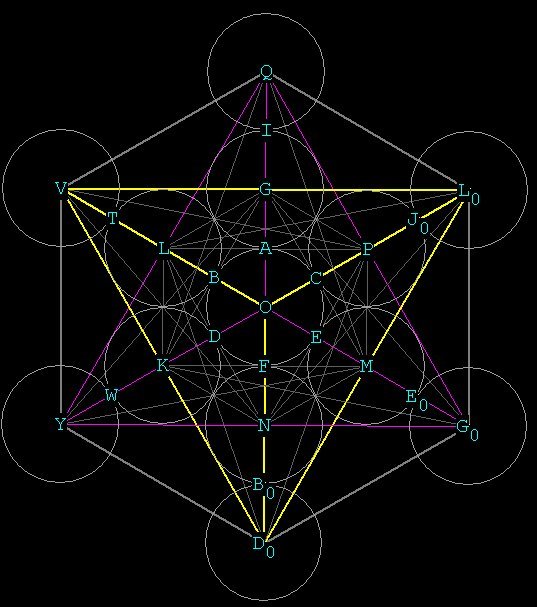
The first tetrahedron is in yellow.
The vertex at O either comes out of the screen or goes into the screen
depending upon how you look at it. The second tetrahedron is outlined
in
green and blue. You can see the cube surrounding the tetrahedrons (look
at vertices Q,V,O, L0. That is the top face of the cube. The bottom
face
is at O,Y,D0,G0). The cube is unstable and if you build one with the
edges
hinged, it will collapse. A cube with 2 tetrahedra inside of it fully
braces
and supports it.
The tetrahedron is the simplest regular solid in the universe and has
been used as the basis for constructing a photon. Fuller used it as the
basic quanta in the construction of the universe.
However, we can see from the pattern that the circle and the sphere are
prior to it. All things which persist must be curved, as we have
pointed out before in earlier essays. Perfectly straight lines cannot
exist in nature because they do not persist. Therefore, all polyhedra
(3 dimensional solids) are actually relationships between the nodes.
The faces and the edges don't really exist except in our minds, as a
way to help us see how nodes of energy come together.
As we saw at the beginning of this essay, the sphere comes from the
circle and the circle comes from the decision of consciousness to
occupy a location and rotate a point of awareness around itself.
Therefore, the cretaion of all Forms proceed from the circle and the
sphere.
Next, the octahedron: (the orange sides are to the front.
The blue
sides
are at the back of the figure)
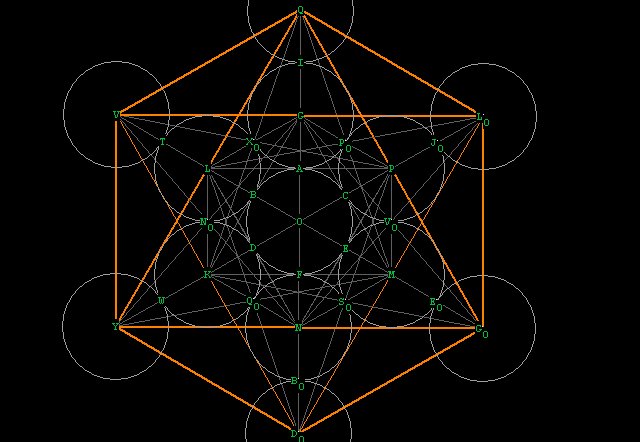
The octahedron again fits precisely into the pattern.
Now, the icosahedron:
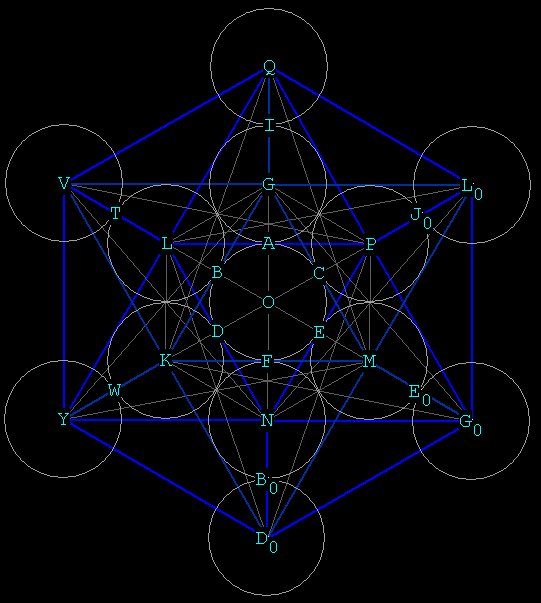
It looks like the points fit nicely into the pattern at
all of the
sphere
centers, but this is not so. QY, for example, is divided at L in
extreme
and mean ratio, and QV is actually divided in EMR as well, but this pic
doesn't show it, because QV actually travels down further into the
sphere
than I can show here. This is true for all of the vertices of the
icosahedron,
except for the top and bottom POINTS at Q and D0. All of the
coordinates
of the icosahedron involve Ø.
Even though the Icosahedron does not
fit directly into the pattern, this Phi based Platonic Solid can be
generated from the Octahedron or the Cube, which fits perfectly.
The Icosahedron can be generated from
the Octahedron by dividing its sides in Mean and Extreme (Phi) Ratio:
The Icosahedron can be generated from the Octahedron which fits
perfectly into the Pattern.
Why does the icosahedron have problems fitting into the
sphere
pattern?
Because it is composed of pentagons!
All of the faces of the icosahedron are equilateral triangles (for
example, NPL) but you will notice that it can also be considered to be
made of pentagons. JKHIG is a pentagon, for example, and so is OHRNG.
In fact, the Icosahedron is made up of pentagons AND equilateral
triangles!
The ratio of the radius of the icosahedron to the length of its side
involves Ø. More on that when we analyze the icosahedron in
detail.
The icosahedron has a pentagonal sub-structure, and so it is one of
those polyhedra associated with life. The icosahedron is always
striving
toward perfection, toward that perfect division into EMR, and so
contains
the internal dynamic tension common to all biological life.
Fuller has shown that if you remove the central sphere in an
arrangement
of closest-packed (tangent) spheres called the vector equilibrium or
cube-octahedron,
the icosahedron can form nicely from all of the sphere centers. He
called
this the 'jitterbug' transformation. Perhaps this is how life gets the
idea of how to make the pentagon.
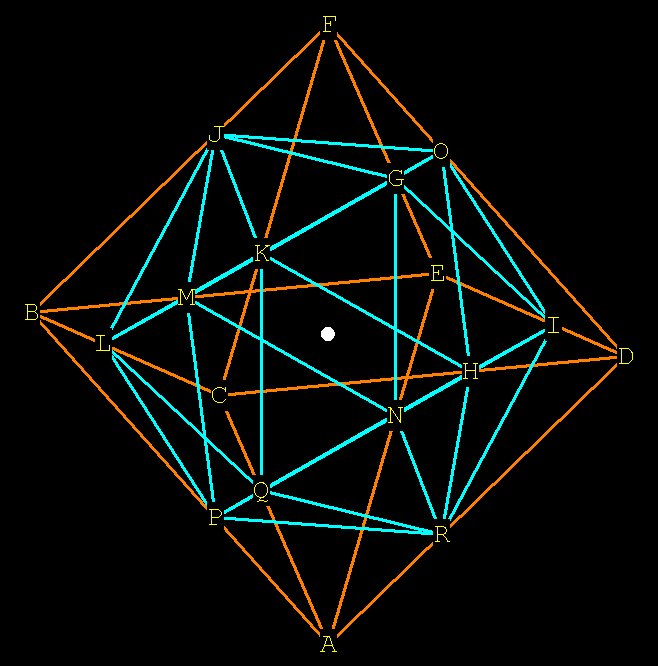
Finally, the dodecahedron:
The intersection of the LINES of communication between sphere centers
create more POINTS which can be used to build the dodecahedron.
These lines divide themselves into EMR, but never of course perfectly.
You can see that the vertices of the dodecahedron are not at easily
identifiable
places within the structure.
The dodecahedron is composed entirely of pentagons. It is therefore
the most dynamic of all of the regular polyhedra. There is more energy
within the structure, more tension, as it constantly strives for the
perfect
division.
The ratio of radius of the sphere enclosing the dodecahedron to the
length of the dodecahedron's side also involves Ø. Somehow
this structure must be intimately associated with biological life.
The Dodecahedron can also be formed indirectly from
pattern by using the Cube, and it's vertices can be found by orienting
5 Tetrahedrons, like so:
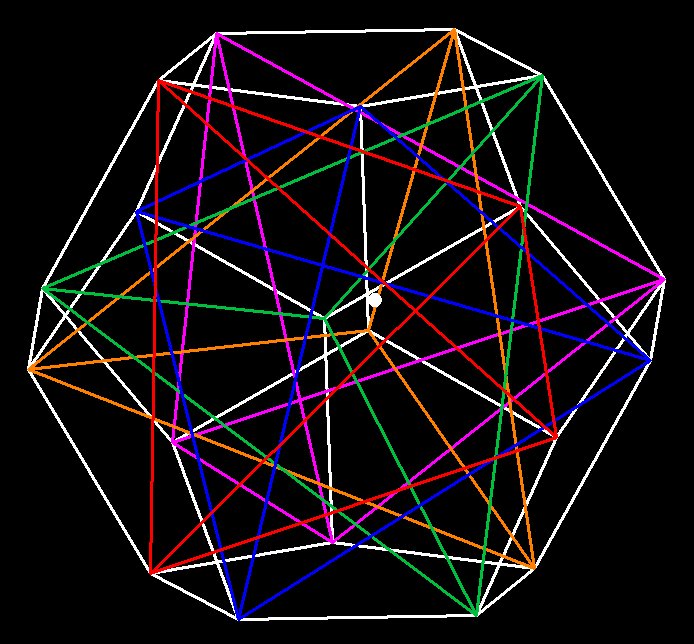
The Dodecahedron is even more difficult to contruct because
it is composed entirely of pentagons. For that reason, this structure
must be intimately associated with biological life.
The main idea is that we can make any possible geometric
shape, either directly, or indirectly, from
the intersecting sphere pattern. (I have just shown the 5 regular
solids
here).
Even though the dodecahedron and the icosahedron must always remain
slightly imperfect (or any shape which has Ø within its
makeup),
by altering the radius of the spheres and superimposing
interlocking
sphere patterns one over the other, all of the forms we observe in
existence
can be constructed.
_________________________________________________________________
(0) Geometric drawings done using R. Parris's free
'peanut'
software
at http://math.exeter.edu/rparris/default.html
(1) GIF animation by Ed Stephan (stephan@cc.wwu.edu) from
U.S. Naval Observatory page at:
(2) http://tycho.usno.navy.mil/vphase.html
(3) ref "The Ancient Secrets of the Flower of Life" by Drunvalo
Melchizedek.
This is a very interesting and informative book, but rather on the
wild side. I enjoyed the geometry in it, but I can't say I subscribe to
some of the way-out theories presented as explanations for earth
history.
You will have to judge for yourself the validity of the information. I
highly recommend it as a way to loosen up your mental horizons, and to
make you question the dogmas of present day science. The
book
is Part One of a series of lectures describing background data to a
very
powerful meditation, which I have had very good results with.
(4) from http://www.dnaftb.org/dnaftb/ Section 15 of 'DNA From
the Beginning'.
(5) from http://mathworld.wolfram.com/Torus.html, "Eric Weisstein's
World of Mathematics"










 (5)
(5)

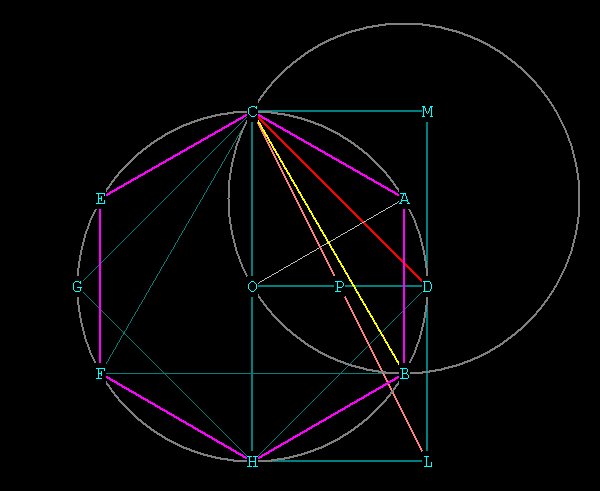
 (4)
(4)








