The Dihedral Angle of the Icosa–Dodecahedron
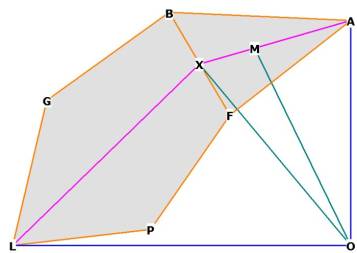
Figure 1 --- The dihedral angle of the icosa–dodecahedron
Consider Figure 1. We see that the dihedral angle is LXA, being the intersection of the 2 planes
BGLPF and FBA. I have drawn the line LXA which goes directly through the middle
of both planes and forms a 'roof' over them.
If you build an icosa–dodecahedron you will see immediately that the angle from
A to the centroid O and back to L, or LOA, is right.
LO = AO = radius of enclosing sphere = * ids.
Our plan of attack for getting LXA will be as follows:
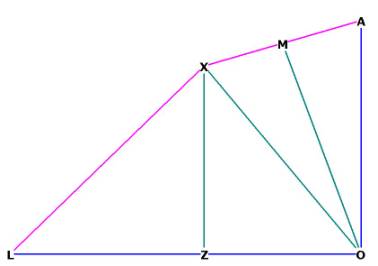
Figure 2 --- dihedral angle, revisited
Note that ZX is drawn parallel to OA, and thus also
perpendicular to LO.
Therefore XZO and XZA are right.
AM and MX are the distances, respectively, from the vertex of an
equilateral triangle to the mid-face, and from the mid-face to a mid-edge.
From Equilateral Triangle , we know these to be
XL is also known, being the height of a pentagon.
From Pentagon Construction we know this distance to be
In Figure 2, the line OM is drawn perpendicular to the triangular face at its midpoint. Therefore the angle OMA and the angle OMX are right.
Note that from the above data, we can conclude that the
triangles
OMA, OMX, XZO and XZL are right.
OM can be determined because we know OA and AM.
Therefore the angle MOA can be calculated.
With OM and MX known, OX can be determined, because triangle OMX is right.
Therefore the angle MOX can be calculated.
Now AOX is known, and we can get XOZ, because we know LOA is right.
Because triangle XZO is right, and we know XOZ, the angle ZXO can be calculated.
Now we know the angle ZXA, it being the sum of ZXO and OXA.
Now we are left with triangle LZX, which is right by construction.
XZ can be determined from the data in triangle XZO, and then ZXL can be calculated from triangle LZX.
The dihedral angle LXA is then the sum of ZXL and ZXA.
That was quite a lot of work, but now the fun stuff is done, which for me is figuring out the geometry. Now it's just a bunch of calculations!
Our work is made easier because we can get the distances OM
and OX from our previous calculations in Icosa–Dodecahedron. OM is just the
distance from the centroid of the i.d. to mid–triangular face, and OX is just
the distance from the centroid to any mid–edge.
We determined OM = and OX =
Let's get going!
sin ( MOA) = AM / OA =
MOA = 20.90515744°.
tan ( MOX) = MX / OM =
MOX = 10.81231696°.
XOA is therefore MOA + MOX = 31.71747441°.
Well, well well. Here we recognize an angle which is a part
of our good friend the Phi Right Triangle with sides divided in Mean and
Extreme Ratio.
Triangle XOA is not right, but triangle XZO is.
Since LOA is right,
LOX = ZOX = LOA - XOA = 90 - 31.71747441 = 58.28252559°.
Therefore ZXO = 31.71747441° and triangle XZO has sides
divided in Mean and Extreme Ratio.
Therefore we know XZ / OZ = Ø.
Now
tan( OXM) = OM / MX =
OXM = 79.18768304°. (Note: We could also have
calculated OXM using the following reasoning: Because
triangle OMX is right,
OXM = OXA = 180 – 90 – 10.81231696° = 79.18768304°)
So ZXA = ZXO + OXM = 110.9051574°.
Or more precisely, ZXA = arctan( )+ arctan ( )
We are almost there.
If we can find ZXL, we can finally determine LXA.
We know XL. We need to get either LZ or XZ.
Lets get LZ.
LZ = LO - ZO. What is ZO?
To determine that, we need OX, which we already know.
Now we can write:
cos( ZOX) = ZO / OX, ZO = OX *
cos( ZOX).
We know that triangle XZO is a triangle and so
cos( ZOX) =
So ZO = .
Now since LO = radius = ,
then LZ = LO - ZO =
Therefore LZ = ZO.
sin( ZXL) = LZ / XL =
ZXL = 31.71747441°.
So the dihedral angle LXA = ZXL + ZXA =
110.9051574° + 31.71747441° = 142.6226318°.
Note that OX = XL and so triangle XZO congruent to triangle XZL.
Triangle XLO is isosceles.
XL / LZ also equals .
