The Rhombic Triacontahedron
The Rhombic Triacontahedron is an extremely fascinating polyhedron. It is
built around the dodecahedron, and like the dodecahedron, it has many phi
relationships within it. This polyhedron contains all five of the Platonic
Solids directly on its vertices, and shows the proper relationship between
them.
The Rhombic Triacontahedron (hereinafter referred to as r.t.) has 30
faces, 60 edges, and 32 vertices.
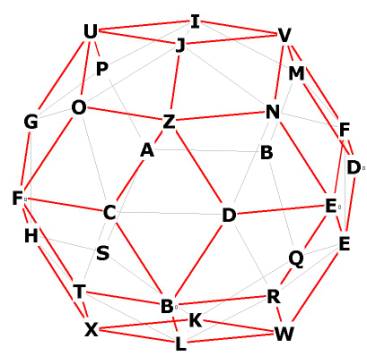
Figure 1 -- showing the front portion of the Rhombic Triacontahedron (red) with
the sides of the dodecahedron (gray)
Notice pentagon CDNJO, then notice Z. Z is raised off the pentagon (a
distance we shall find later on) and Z is connected to all 5 vertices of the
pentagonal face of the dodecahedron. This can be seen even more clearly at U.
The pentagon GPIJO has all of its vertices connected to U. Of course, we could
have drawn this figure without the dodecahedron faces, which is obviously not
part of the r.t., but it helps for clarity.
Notice that the faces of the r.t. are diamond-shaped, somewhat like the rhombic
dodecahedron, but these faces are longer and skinnier. Look at the r.t. face
UOZJ at the upper left. U and Z are the long-axis vertices. Notice that
the line between O and J, the short-axis vertices, form one of the edges
(sides) of the dodecahedron.
The dual of the r.t. is the icosa-dodecahedron.
The r.t. is more clearly spherical than any of the polyhedra we have studied so
far.
Notice also: In Figure 2 below, we see that the rhombic triacontahedron has
internal pentagonal planes just like the icosahedron and the dodecahedron!
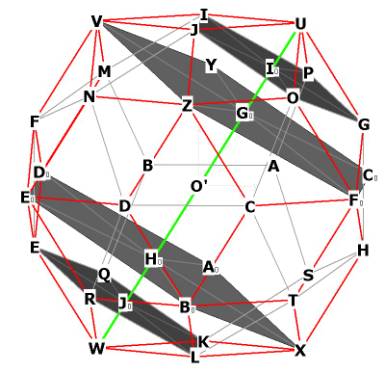
Figure 2 -- showing the internal pentagonal planes of the r.t. Figure 2 is
rotated 180 degrees with respect to Figure 1.
Note the large highlighted pentagons. The lengths of all of the large
internal pentagon sides are precisely the long axis of every r.t. face! For
example, look at VZ and ZFo in the top pentagonal plane and EoBo in the lower
pentagonal plane.
The r.t. has a circumsphere and an inner sphere. The circumsphere goes around
all 20 of the vertices that rise off the faces of the dodecahedron.
The diameter of the circumsphere is UW. UW is in green in Figure 2. O' is the
centroid. The circumsphere touches all
of the vertices that are raised off the pentagonal planes of the dodecahedron.
There are 12 of these, because there are 12 faces on the dodecahedron.
The inner sphere touches all of the 20 vertices of the dodecahedron. The
diameter of the inner sphere would be, for example, IL. UW > IL.
This leads us to think that possibly, the relationship between U, Go,O',Ho and
W will be similar to those of the dodecahedron and the icosahedron. Later
on, we will see that this is indeed the case.
Notice also that the rhombic triacontahedron inherently contains within it
not only a dodecahedron, but an icosahedron as well! Notice that the 12
vertices which rise off the dodecahedron faces provide the 12 vertices of the
icosahedron. Remember that the dual of the dodecahedron is the
icosahedron and that the dual is formed by taking points at the center of the
faces.
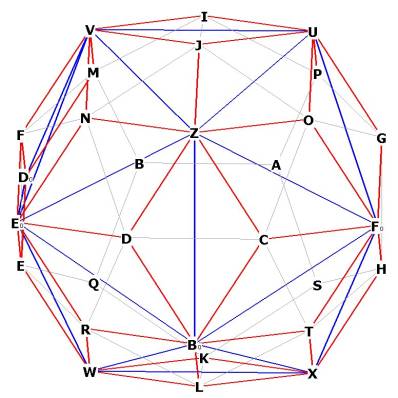
Figure 3 -- showing the 12 vertices of the icosahedron (blue) within the
rhombic triacontahedron
The sides of the icosahedron are the long axes of the r.t. faces.
The sides of the dodecahedron are the short axes of the r.t. faces.
Therefore the rhombic triacontahedron is just the combination of the
dodecahedron with its dual, the icosahedron.
The rhombic triacontahedron is the model nature uses to demonstrate the
true relationship between the side of the icosahedron and the side of the
dodecahedron. We will see later on that these relationships are based on 
.
Note also that when a cube is inscribed within 8 of the 12 vertices belonging to the dodecahedron within the rhombic triacontahedron, the lengths of the cube sides are precisely equal to the long axis of any of the rhombic triacontahedron rhombi. Furthermore, the sides of the cube are precisely equal to any of the diagonals of the pentagonal faces of the dodecahedron:
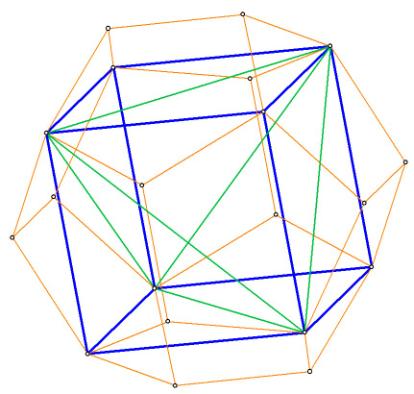
Figure 3A
The sides of the cube, in blue, are also the diagonals of the pentagonal faces
of the dodecahedron within the rhombic triacontahedron.
Since the tetrahedron (one tetrahedron in green, the other in purple) and the
octahedron (in orange) can be inscribed within the cube, the rhombic
triacontahedron shows the precise relationship between the Platonic
Solids!
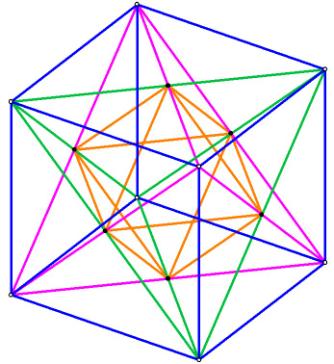
Figure 3B -- The cube, 2 interlocking tetrahedrons, and the octahedron inside a
cube
The Rhombic Triacontahedron therefore elegantly describes the nesting of the five Platonic Solids: icosahedron, dodecahedron, cube, tetrahedron, octahedron. When the sides of the octahedron are divided in Mean and Extereme (Phi) Ratio, another icosahedron is formed. This begins the process all over again, and shows that the 5 nested Platonic Solids may not only grow and contract to infinity, but do so in a perfectly harmonious way.
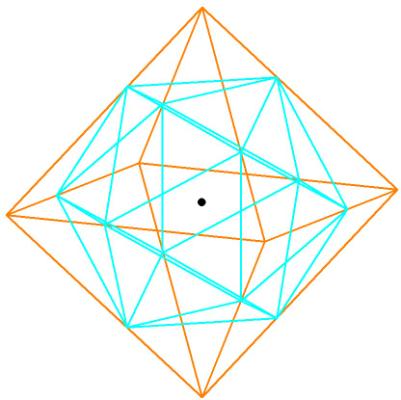
Figure 3B -- Showing how the icosahedron nests within the octahedron. Interestingly, the icosahedron is formed within the octahedron by dividing each edge of the octahedron in Phi Ratio.
What is the volume of the rhombic triacontahedron?
As before we use the pyramid method. There are 30 faces, so there are 30
pyramids. Imagine a point at the very center of the r.t. If you connect that
point up with one of the faces, you will have a pyramid that looks like this:
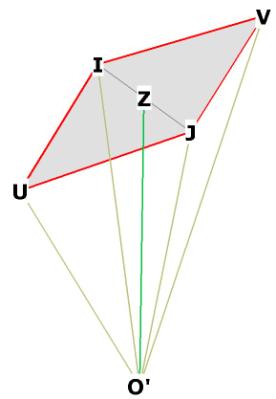
Figure 4 -- one of the 30 pyramids of the rhombic triacontahedron. O'Z is the
height of
the pyramid. O'U = O'V = radius of outer sphere which touches the 12 r.t.
vertices which are raised off the center of the dodecahedron face. O'I = O'J =
radius of inner sphere which touches all 20 of the short-axis r.t. vertices,
which are also the vertices of the dodecahedron
We want to find the volume of the r.t. in terms of the r.t. side. However,
we don't know the length of the r.t side! But we do know the length of the side of the dodecahedron, in terms of a
unit sphere which touches all the vertices of the dodecahedron. So let's try to
get the r.t. side (hereinafter referred to as rts) in terms of the dodecahedron
side.
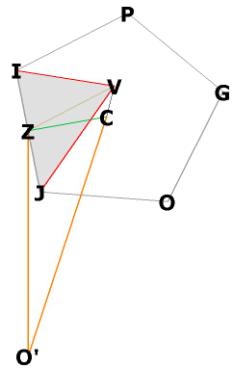
Figure
5
Figure 5A
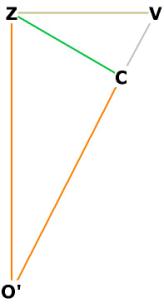
Figure 5 and 5A show the following important data:
V is one of the 12 raised vertices of the r.t. off the face of the
dodecahedron.
C is the center of the dodecahedron face. C lies in the plane of IJOGP, and is
directly below V.
Z is the center of the r.t. face IUJV (see Figure 4), and also the mid-edge of
the side of the dodec.
IVJ (in red) is one-half of the r.t. diamond face IUJV (see Figure 4)
O'Z is the distance from centroid to mid-edge of the dodec face. This is the
height of the r.t. pyramid.
ZV is the distance from mid-edge of dodecahedron to the raised vertex V off the
dodecahedron face.
ZC is the distance from mid-edge of dodecahedron to center of dodecahedron
face.
CV is the distance of V off the center of the dodecahedron face.
Figure 5A shows that O'CV is a straight line, so that 
ZO'C = 
ZO'V.
O'ZV is right.
O'CZ is right.
From this data we can show that the triangles O'ZV, O'CZ, and CZV are
similar by angle-side-angle.
First we show the triangle O'ZV and O'CZ are similar:
O'ZV is right, so is O'CZ.
O'Z is common to both triangles.
ZO'V = 
ZO'C. Therefore both triangles are
similar by ASA.
Now we show that triangle CZV is similar to triangle O'ZV by
angle-side-angle.
ZCV and 
O'ZV are right.
ZV is common to both triangles.
O'VZ = 
CVZ.
Therefore both triangles are similar by angle-side-angle.
With this information we can determine CV, the distance of the vertex V off
of the dodec face, and ZV, which will enable us to get the side of the r.t. in
terms of the side of the dodecahedron.
Since all 3 triangles are similar, we can write the following relationship:
CZ / O'C = CV / CZ.
The distances O'Z, O'C, and CZ are known. From Dodecahedron
it is known that
(ds means dodecahedron side)
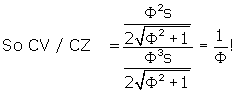
Now we have CV, the distance from the plane of the dodecahedron to the rhombic
triacontahedron “cap” over the dodecahedron face, in terms of the dodecahedron
side.
Now we need to find ZV, so that we can get IV, the length of the side or
edge of the rhombic triacontahedron. We can write the following relationship:
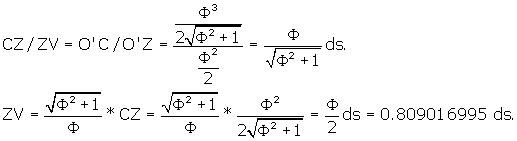
Refer back to Figures 4 and 5. Now that we have ZV, we can find the side of
the r.t., IV.
The triangle IVJ in Figure 4 and 5 is one-half of an r.t face. We have already
calculated ZV, and we know that IZ is just one–half the side of the side of the
dodecahedron, ds. We also know that the angle IZV is right by
construction.
Therefore, by the Pythagorean Theorem,
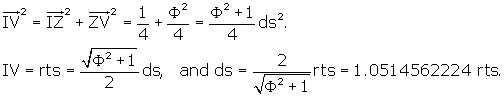
Here we have established an important fact: we have related the side of the
rhombic triacontahedron, or rts, to the side of the dodecahedron and,
therefore, to the radius of the unit sphere which encloses all 20 vertices of
the dodecahedron and, in turn, the short axis vertices of the rhombic
triacontahedron.
We can now describe the distance of any vertex of the r.t. off the plane
of the dodecahedron, CV, in terms of
the side of the r.t. We may now write
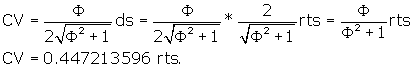
Let's now find the radius of the outer sphere of the r.t. in terms of the side of the r.t. itself. Remember that the outer sphere touches all 12 long-axis vertices of the r.t., and that these 12 vertices are the vertices of an icosahedron
We need to convert these distances so that they are
related to rts, not ds.
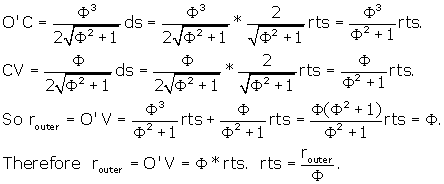
In the Rhombic Triacontahedron, the relationship between the side and the radius of the enclosing sphere is Phi.
What is 
? This is just the unit sphere which touches all 20 vertices
of the dodecahedron. We know from Dodecahedron
that 
Converting this to the side of the r.t. we have:
Now we have enough information to calculate the volume of the rhombic
triacontahedron in terms of it's own side. Refer back to Figures 4 and 5 for
diagrams.
We can calculate the area of the r.t. face, because we know IJ and ZV, which we
can use to give us the area of one-half the face of the r.t. We see from Figure
4 that O’Z, the height of the r.t. pyramid, is just the distance from the
centroid to the mid-edge of any of the sides of the dodecahedron. We know from Dodecahedron, that this
distance is
. We have to do some conversions of these values first, to
get them all in terms of the rts.
To get the area of the r.t. face, divide it into 2 identical triangles at
the short axis IJ, find the area of one triangle, and multiply by 2..
The area of any triangle is 1/2 * base * height, so the area of the r.t. face
is twice this value.
IJ is just the side of the dodecahedron, and it is the base of our triangle.
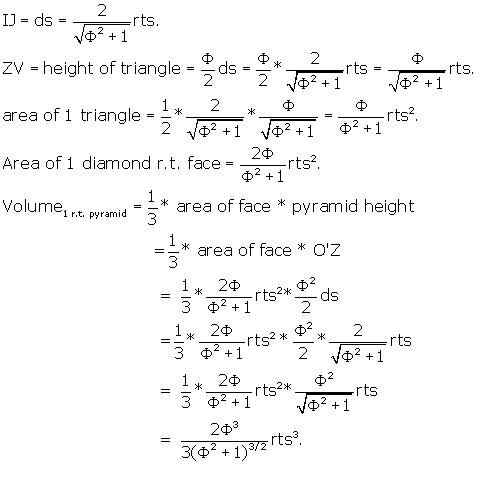
There are 30 pyramids for 30 faces so total volume 
is:
The volume of the r.t. can be calculated another way. Since the r.t. is
built upon the dodecahedron, the r.t. volume is just the volume of the
dodecahedron + the extra volume of all of the little 12 pentagonal pyramids
formed from the raised vertices off the 12 pentagonal faces of the
dodecahedron. To see this, check Figure 1 again and look at U-IJOGP or V-
IJNFM.
The volume of the dodecahedron is, from Dodecahedron
,
Converting this to the side of the r.t. we get:
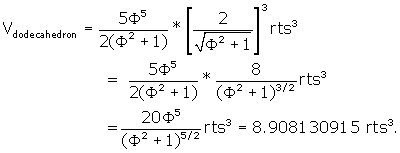
The volume of each of the 12 "extra" pyramids =
1/3 * area of pentagon * CV (height of each raised vertex off of
the face of the dodecahedron) =
We only have one problem: one of our values is in terms of the dodecahedron
side. We need to convert that to the side of the r.t.
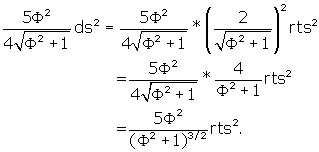
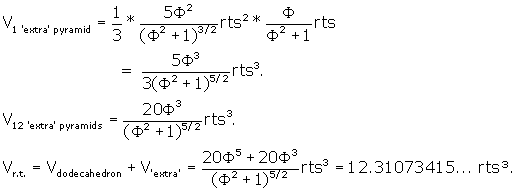
What is the surface area of the rhombic triacontahedron?
Before we calculate the central and surface angles of the rhombic
triacontahedron, let us complete our research into the distances from the centroid
to various points of interest on this polyhedron.
We have already calculated the distances to the small and large axis vertices,
and to the mid-face. Now we need to find the distance from the centroid to any
mid-edge.
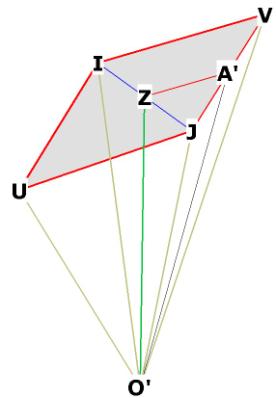
Figure 4a
Showing the right triangle O’ZA’
We are looking for OA’. We may write
. We know O’Z, but what is ZA’?
IZ = ½ IJ by construction.
JA’ = ½ JV by construction.
The triangles VIJ and ZA’J are congruent by angle-angle-angle. Triangle VIJ is
isosceles by construction, therefore triangle ZA’J is isosceles and ZA’ = ½rts.
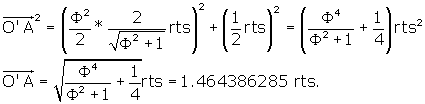
What are the central angles of the rhombic triacontahedron?
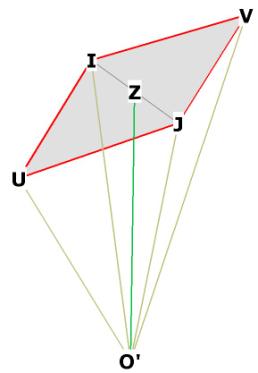
Figure 4, repeated
There are 3 central angles of the r.t. that are of interest. Refer to Figure 4.
The first is UO'V, central angle of the long-axis
The second is IO'J, central angle of the short-axis.
The third and primary central angle is IO'V, the central angle of each adjacent
side.
O'Z is perpendicular to IJ, and to the plane of the r.t. face, IUJV.
O'Z bisects IJ at Z.
Triangles UO'Z and VO'Z are right.
So we can write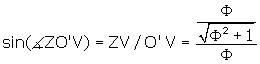 
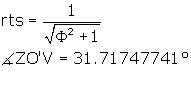
We recognize this angle (see Phi Ratio Triangle ) as
being part of a 
ratio triangle.
The ratio's of these distances are shown below in Figure 6:
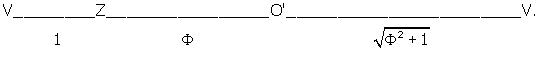Figure 6 --- showing the relationship between VZ, O'Z, O'V
Now 
UO'V = 2 *
ZO'V, so
UO'V = 63.4349488°.
Let's find IO'J, the central angle of the small axis of the r.t. face.
IO'Z and ZO'J are right. So we write
We know IZ = one half the side of the dodecahedron, or 1/2 * ds.
From above we know that 
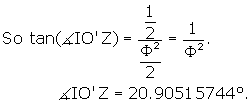
Therefore <IO'J = 2 *
IO'Z = 41.81031488°.
Note that IZ / O’Z =
, so that IZ and O’Z have a relationship based on the square
of 
.
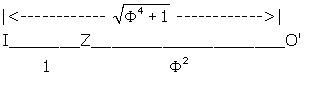
Figure 7 -- showing the relationship between O'Z, IZ and O'I
This division is in ratio 
.
To find IO'V, recognize that the point V lies in a straight line directly
above the center of the dodecahedron face. So the angle from IO'V is the
same as the angle from I to O' to a point (G) in the middle of the dodecahedron
face.
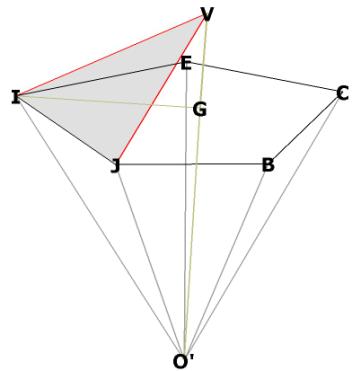
Figure 8 -- showing that the central angle IO'V = the angle IO'G
The triangle O'GI is right by construction, so we need only to know GI and
O'G.
We know from Area of the Pentagon that
,
and from Dodecahedron we know the distance 
.
What are the surface angles of the rhombic triacontahedron?
Observe from Figure 4 that the angles we are looking for are 
IVJ and 
UIV.
Z is a bisector of IZ so the triangle IVZ is right.
IV = the side of the r.t. = rts.
, which we already found above.
So we can write
.
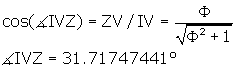We recognize immediately, from The Phi Triangle
, that this angle indicates a right triangle whose long and short sides are
divided in Extreme and Mean Ratio (Phi ratio).
Therefore 
And so the ratio between the long axis VU and the short axis IJ (see Figure 4)
must also be in Mean and Extreme Ratio.
Therefore VU / IJ = 
.
So the face of the rhombic triacontahedron is a 
rhombus.
The face angle we want, 
IVJ, is then twice 
IVZ.
IVJ = 63.43494882° = short axis face angle.
One-half of the other face angle, 
ZIV, is just 90 - 
IVZ = 58.28252558°.
So 
UIV = 116.5650512°.
What are the lengths of the long axis VU and the short axis IJ of the r.t.
face?
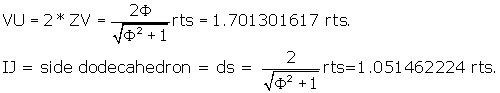
As stated above,
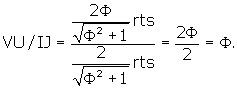
What is the dihedral angle of the rhombic triacontahedron?
To see this calculation, click on R.T. Dihedral
Angle .
The dihedral angle = 144°.
The distance from the centroid to any of the 12 long-axis vertices above the
dodecahedron faces = 
Distance from centroid to any of the 20 short-axis vertices = 
.
We need to go back to Figure 2 now and look at the diameter of the sphere
which encloses the 12 long-axis vertices of the icosahedron. This line is shown
in Figure 2 as UO'W. The diameter passes through the centroid at O' and also
through the middle of the 2 large pentagonal planes marked in Figure 2.
It also passes through the top and bottom faces of the dodecahedron. These
faces are also marked in Figure 2.
There are 4 highlighted pentagonal planes along the diameter UW, as well
as the midpoint O'.
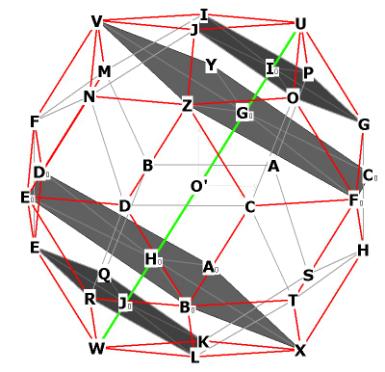
Figure 2, repeated
We have the extra distance off the top plane of the dodecahedron to the vertex
U, marked as IoU, and the extra distance off the bottom plane of the
dodecahedron to the vertex W, marked as JoW.
What are the relationships between U, Io, Go, O', Ho, Jo, and W?
In Figures 5 and 5A, we found the distance off the plane of the dodecahedron
face (IoU , JoW ) to be CV.
CV we found to be 
So IoU = JoW = 
Refer back to Figure 2.
Let's find the distance UGo, or the distance from U to the first large
pentagonal plane VYCoFoZ.
This will be easy, because we know that the sides of this pentagonal plane are
just the long axes of the r.t. We can form a right triangle from U to any one
of the vertices of VYCoFoZ, to the center Go. Let's take the right triangle
UGoZ. From Construction of the Pentagon
we can get GoZ, it is just the distance from pentagon center to one of the
vertices. Inspection of Figure 2 shows that UZ is just the long axis of the
r.t. face UJZO.
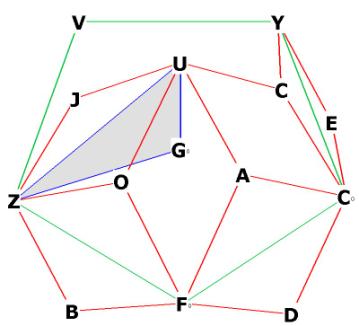
Figure 9 -- showing the large internal pentagon VYCoFoZ and the right triangle
UGoZ.
Go is the center of the large internal pentagon. U is directly above Go.
The sides of the large pentagon (in green) are all long axes of the r.t. faces,
indicated in red.
Triangle UGoZ is right by construction.
or long-axis of r.t.
face.
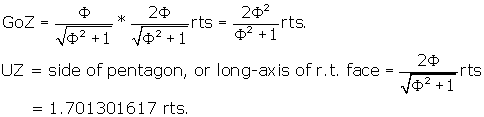
Now we can find UGo:
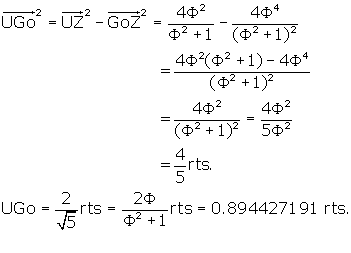
So UGo = 2 * UIo and the plane VYCoFoZ of the dodecahedron is twice
the distance from U as is the large internal pentagonal plane IPGOJ.
That means UIo = IoGo = 1/2 UGo = 
What is the distance between the centroid O' and the plane IPGOJ, or O'Go?
It is O'U - UGo.
We know O'U, it is the radius of the outer sphere, or 
Therefore,
Now we have enough information to make our distance chart of internal planar distances of the rhombic triacontahedron, just as we did for the icosahedron and the dodecahedron.
Table 1.
Distances between internal planes of the rhombic triacontahedron.
Table 2. Relationships between
distances in Table 1.
(included in the book)
From the table of relationships we see that:
O'Io is divided in Extreme and Mean Ratio at Go.
O'Jo is divided in Extreme and Mean Ratio at Ho.
UHo is divided in Mean and Extreme Ratio squared at Go.
WGo is divided in Mean and Extreme Ratio squared at Ho.
Conclusions:
The rhombic triacontahedron is a combined icosahedron-dodecahedron
dual, so it is not surprising to see so many relationships based on the
division in Mean and Extreme Ratio.
The rhombic triacontahedron contains all of the properties of the icosahedron
and all of the properties of the dodecahedron and it tells us the proper
nesting order of the 5 Platonic Solids.
Dihedral Angle Of The Rhombic
Triacontahedron
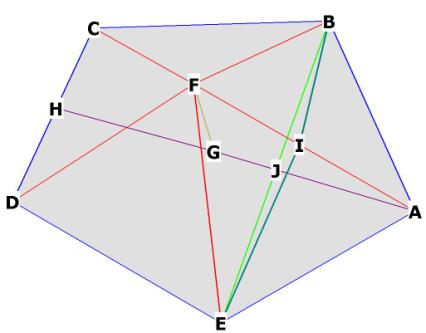
Figure 1. We are looking for the dihedral angle, 
BIE . Figure 1 shows an r.t. “cap” (in red) over the face of
the dodecahedron, and shows that J and G are on AH, the height of the pentagon.
F is directly above the mid-face of the pentagon, at G. I is directly
above J on BE. 
BJI is right, allowing us to calculate 
BIJ or 
EIJ, and 
BIE, the dihedral angle, is then just twice that.
AH and BE lie on the pentagonal plane ABCDE.
BI is a line along an r.t. face, EI is a line along another of the faces.
Here is our plan of attack:
We know from Rhombic Triacontahedron that 
BFA is 63.43494882° This can be rewritten without loss of
information as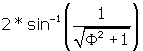 
. Triangle BIF is right by construction. BF is the side of the
r.t., or rts. Here we must use trigonometry to get BI, by taking the sine of 
BFA so we can find BI. BE is bisected by AH, the angle
bisector of 
BAE and a diagonal of the pentagon. AJ is known from Pentagon Construction. To get 
BIJ, we can take the sine of 
BIJ = BJ / BI. The
dihedral angle 
BIE is twice angle BIJ.
First let’s find BJ. BJ is one-half the
diagonal of the pentagon with sides equal to the side of the
dodecahedron. We must change units in terms of the side of the r.t. Remember
that 
So we write BJ = 
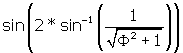= BI / BF.
BI = BF *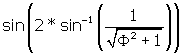 
.
BI =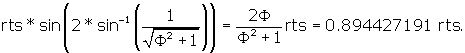 
Now we can calculate the dihedral angle BIE.
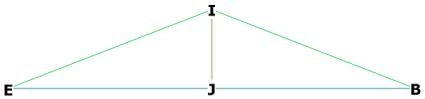
Figure 4 The dihedral angle BIE
We can write
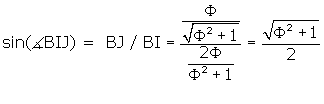
BIJ = 72°.
The dihedral angle BIE is 2 * 
BIJ.
Dihedral Angle = 144°.
Return to Rhombic
Triacontahedron
Return to Geometry Home Page The Big Picture Home
Rhombic
Triacontahedron Reference Tables
(Included in the book)
