The
Tetrahedron

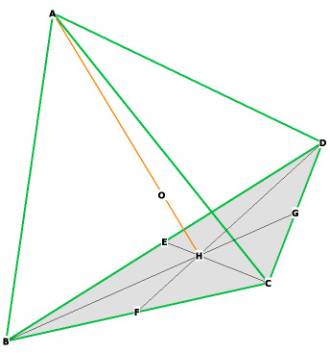
Figure 1
Each side of the tetrahedron is in green. We will refer to
the side or edge of the tetrahedron as ‘ts.’
The tetrahedron has 6 sides, 4 faces and 4 vertices. In Figure 1 the base is
marked out in gray: the triangle BCD. Each of the faces is an equilateral
triangle.
From The Equilateral
Triangle we know that:
Area BCD = ![]() .
.
Now we need to get the height of the tetrahedron, AH.

Figure 2
From The
Equilateral Triangle we know that:
BH = ![]() .
.
Now that we have BH, we can find AH, the height of the
tetrahedron. We will call that h.
![]() =
= 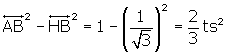 .
.
![]()
![]() = 1/3 * area BCD * h =
= 1/3 * area BCD * h = ![]()
What is the surface area of the tetrahedron? It is
just the sum of the areas of its 4 faces.
We know from above that the area of a face is ![]() .
.
The total surface area of the tetrahedron = ![]() .
.
We have found the volume of the tetrahedron in relation to it's side.
Since all 4 vertices of the tetrahedron will fit inside a sphere, what is the relationship of the side of the tetrahedron to the radius of the enclosing sphere
It's easier to see the radius of the enclosing sphere if we
place the tetrahedron inside a cube:
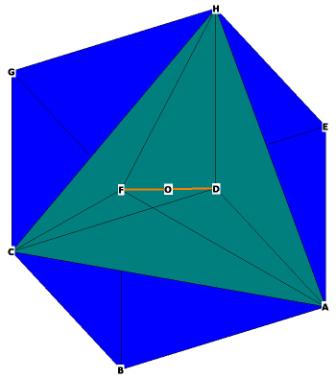
Figure 3
The 4 vertices of the tetrahedron are H,F,C,A.
The 4 faces of the tetrahedron in this picture are: CFH,CFA,HFA, and at the
back, HCA.
(The vertex D is a part of the cube, not the tetrahedron).
The vertices of the cube all touch the surface of the sphere. The diameter of
the sphere is the diagonal of the cube FD.
In this analysis and the ones following, we will assume that all of our
polyhedra are enclosed within a sphere of radius = 1. That way we will be able
to accurately assess the relationship between all of the 5 regular solids.
The radius of this sphere is OF = OD = 1. How does the side of the tetrahedron
relate to the radius of the sphere?
The side of the tetrahedron is the diagonal of the cube, as can be seen in
Figure’s 3 and 4.
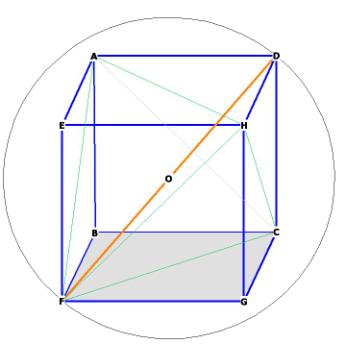
Figure 4
FC is the side of the tetrahedron, DC is the side of the cube, FD is the
diagonal of the cube and the diameter of the sphere enclosing the cube and the
tetrahedron.
By the Pythagorean Theorem, ![]() .
.
![]() , DC = 1.
, DC = 1.
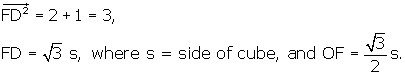
So FG(side of cube), FC(side of tetrahedron), and
FD(diameter of enclosing sphere)
have a 1, ![]() relationship.
relationship.
What is the relationship between the side of the tetrahedron and the radius of the enclosing sphere? We want to know the relationship between OF and FC.
![]() . FD = 2 * OF, so
. FD = 2 * OF, so ![]() . Therefore,
. Therefore, ![]() .
.
So we write ![]() .
.
Where is the center of mass of the tetrahedron? We have
marked it as O in the preceding figures. The centroid is just the distance O to
any of the tetrahedron vertices, or the radius of the enclosing sphere. The
center of mass of the cube is also the center of mass of the tetrahedron; as is
evident from Figure 3 and Figure 7, every vertex of the tetrahedron is a vertex
of the cube.
We already have OF, or r, which is ![]() . If we compare this distance to the height of the
tetrahedron, we get
. If we compare this distance to the height of the
tetrahedron, we get 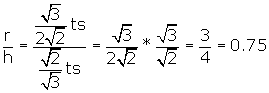
Therefore AO = 3 * OH.
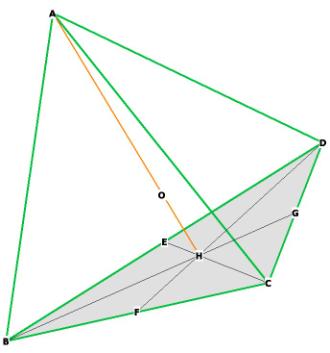
Figure 1, repeated.
Compare this to the equilateral triangle, where the
relationship is 2 to 1.
What is the central angle of the tetrahedron? The central angle is the angle
from one vertex, through the centroid O, to another vertex. This can best be
seen from Figure 3.
vertex
vertex
centroid
Figure 5
We calculate everything in terms of the side of the tetrahedron.
OF = OH = radius of enclosing sphere. FH = ts.
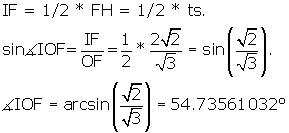
The central angle FOH = 2 * <IOF.
Central angle = 109.47122064![]()
What is the surface angle of the tetrahedron? The surface
angle is that angle made by the angles within the faces. Since each face of the
tetrahedron is an equilateral triangle, the surface
angle = 60![]()
What is the dihedral angle of the tetrahedron?
The dihedral angle is the angle formed by the intersection of 2 planes:
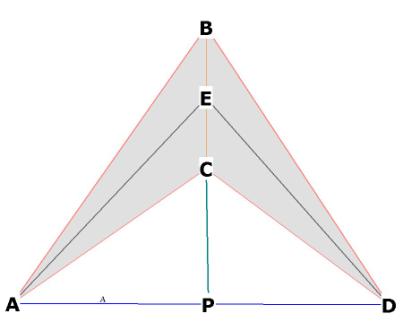
Figure 6
BAC and BDC are 2 intersecting faces of the
tetrahedron. E is at the midpoint of BC.
AE and DE are lines that go through the middle of each face and hit E.
The dihedral angle is ![]() AED.
AED.
The triangle EPD is right. ![]() PED = 1/2
PED = 1/2 ![]() AED by construction.
AED by construction.
AD is the side of the tetrahedron s, so PD = ½ * ts
ED, the height of the tetrahedron face = ![]() .
.
sin(![]() PED) = PD/ED =
PED) = PD/ED = 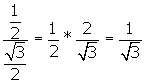 .
.
![]() PED = arcsin (
PED = arcsin (![]() ) = 35.26438968
) = 35.26438968![]()
![]() AED = 2 *
AED = 2 * ![]() PED, Dihedral angle = 70.52877936
PED, Dihedral angle = 70.52877936![]()
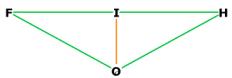
Now we will calculate the distances between the centroid and
1) the middle of one of the faces (OJ)
2) the midpoint of one of the sides (OI)
3) any vertex (OH)
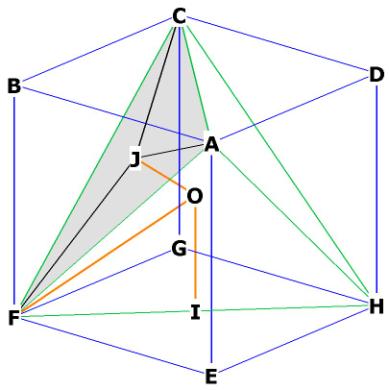
Figure 7, showing centroid distances.
OF = distance from centroid to a vertex, in this case, F,
OI = distance from centroid to middle of a side, in this case, the side FH
OJ = distance from centroid to middle of a face, in this case, face ACF,
The 4 faces are CFH, CFA, HFA and HCA as before. The middle of face CFA is J.
The midpoint of the side of the tetra FH is at I.
We have already figured out OF = OC = OA = OH, the distance from
the centroid to any vertex. This is, as you recall, ![]() .
.
Let's get OI first.
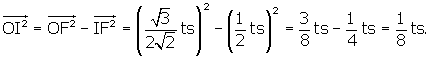
OI = ![]()
The triangle FJO in Figure 7 is right because ![]() OJF is right*. This will enable us to get the
distance OJ.
OJF is right*. This will enable us to get the
distance OJ.
From Equilateral
Triangle we know that ![]() .
.
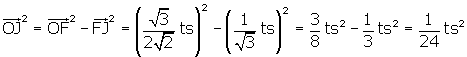 ,
,
OJ = ![]() .
.
To get a good idea of relative distances,
re write OF as ![]() and OI as
and OI as ![]() .
.
Then the relationship between OJ, OI and OF is 1, ![]() , 3.
, 3.
___________________________________________
· Note to teachers: if you build an octahedron and a rhombic dodecahedron off the octahedron faces (use the Zometool), and then attach a tetrahedron off one of the octahedron faces, the centroid of that tetrahedron will be the vertex of the rhombic dodecahedron. In fact, the distance from the centroid of the tetrahedron to each of it’s vertices is the edge length of the rhombic dodecahedron! Nature is not only beautiful, but also logical and consistent.
Return to Geometry Home Page The Big Picture Home
Tetrahedron Reference Tables
(included in the book)
