The Dodecahedron

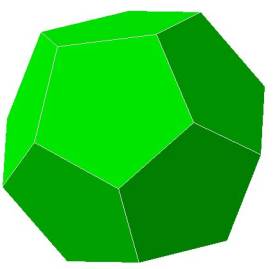
The Dodecahedron

The dodecahedron has 30 edges, 20 vertices and 12 faces. Dodeca is a prefix meaning “twelve.”

The dodecahedron is the only polyhedron I know of which is composed entirely of pentagons.
Buckminster Fuller describes what he calls a '6 pentagonal tensegrity sphere' in Synergetics I, 726.01, and which is shown at Marvin Solit's website at www.fnd.org/geo.htm, but I don't believe that structure can be built without tensegrity struts and tension wires.

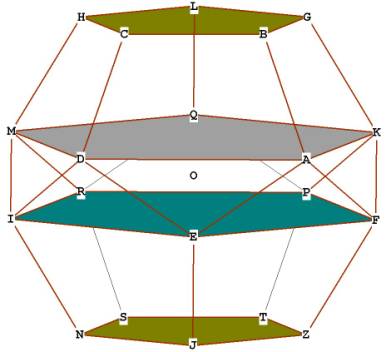
Figure 1
The dodecahedron is pentagonal both inside and out, as can be seen from Figure 1. Like the icosahedron, it has many golden section relationships, which we shall see.
The dodecahedron is even more versatile then the icosahedron. The icosahedron contains and geometry, but the dodecahedron contains , and geometry!

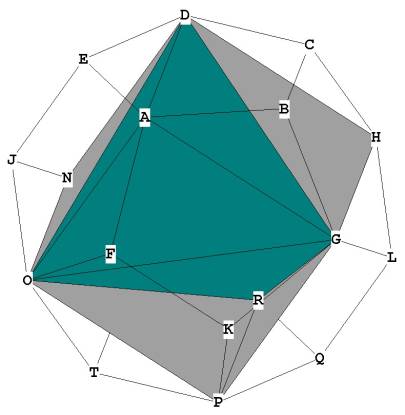
Figure 2
Cube and tetrahedron in dodecahedron. Cube in gray, tetrahedron in green
This view of the dodecahedron is significant in that it shows the 2 dimensional shadow of the decagon. The decagon itself is based upon the pentagon, the building block of the dodecahedron. See Pentagon and Decagon for more information.

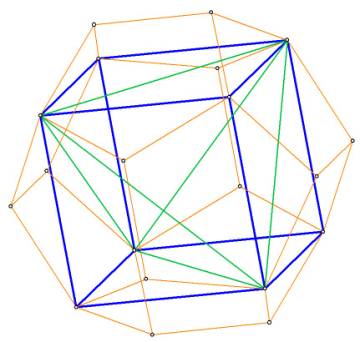
Figure 2A -- Another view of tetrahedron (green) inside cube (blue) inside dodecahedron (orange)

Figures 2 and 2A show how a cube and a tetrahedron can be placed inside a dodecahedron. These placements are 'nice' meaning that the vertices of the placed-in solids are all vertices of the dodecahedron.

The cube, octahedron and tetrahedron are all based on root 2 and root 3 geometry: The relationship of the side of the cube to the radius of its enclosing sphere is r = sqrt(3) / 2.
For the tetrahedron, For the octahedron,
The dodecahedron is capable of elegantly sustaining these and relationships, along with its own many relationships.

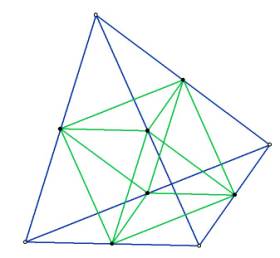
Figure 3 -- octahedron inside tetrahedron
Notice that the octahedron fits precisely on the bisected sides of the tetrahedron.

The icosahedron cannot contain any of the other 5 solids 'nicely' on its vertices.
The icosehedron and the dodecahedron are 'duals' (as are the cube and the octahedron). By 'dual' is meant that if you put a vertex in the middle of all of the faces and connect the lines, you get the dual.
By placing a vertex at the middle of all the faces of the dodecahedron you get an icosahedron, and vice-versa. Figure 4 shows the dual nature of the icosahedron and dodecahedron.

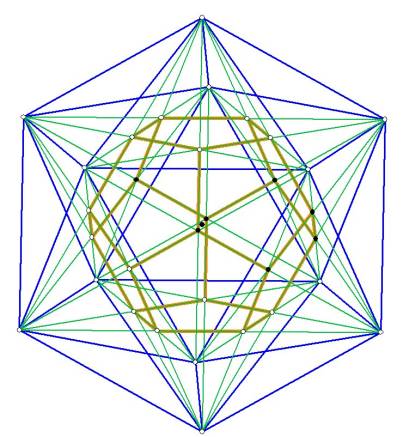
Figure 4 Duals ---- dodecahedron inside icosahedron
Notice that to create the dodecahedron, all we did was draw lines from each vertex of the icosahedron to every other vertex. The vertices of the dodecahedron are at the intersection points. We could just as easily have found the vertices of the dodecahedron by drawing lines on every triangular face of the icosahedron. Where those lines intersect is the center of the face, and a vertex of the dodecahedron. That occurs because the dodecahedron has 12 faces and the icosahedron has 12 vertices.

Now for the standard analysis:
What is the volume of the dodecahedron?
We will use the pyramid method.

There are 12 pentagonal pyramids, 1 for each face, each pyramid beginning at O, the centroid. See Figure 1 and Figure 5.
The volume of any n-sided pyramid is 1/3 * area of base * pyramid height.

First we need to get the area of the base, which is the area of each pentagonal face:

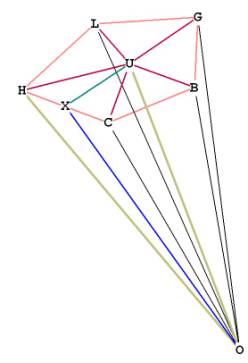
Figure 5 One pyramid on face BCHLG

The area of the pentagon is the area of the 5 triangles which compose it.
From Area of Pentagon we know
This is approximately 1.720477401 .

Now we need to find the height of the pyramid, OU. To do that, we need to find the distance from O to a vertex, lets say, OH. This distance will be the hypotenuse of the right triangle OUH. Since we already know UH, we can then get OU from the good ol’ Pythagorean Theorem.
Imagine a sphere surrounding the dodecahedron and touching all of its vertices. OH is just the radius of the enclosing sphere. If you look at Figure 6, HOZ = GON = diameter. There is a line through HOZ to show the diameter.

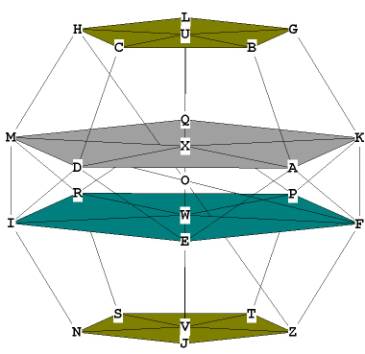
Figure 6

Now look at the rectangle MIFK. The diagonal of it, MF, is also a diameter (MF = HZ). Notice that the long sides of the rectangle, MK, and IF, are diagonals of the two large pentagons ADMQK and FEIRP.
We know from Composition of the Pentagon that the diagonal of a pentagon is * side of pentagon.
We also can see from Figure 6 and more clearly in Figure 1 that the sides of the large pentagons themselves are diagonals of the pentagonal faces of the dodecahedron! (For instance, DA is a diagonal of the face ABCDE). That means each side of the large pentagons is * s and that MK (or any of the diagonals of a large pentagon) is * * s.
So MK = s.
In fact, like the icosahedron, the dodecahedron is composed of rectangles divided in Extreme and Mean Ratio. In the icosahedron, we found these rectangles to be rectangles.
In the dodecahedron, they are rectangles.

In rectangle MKIF, MK = IF = , MI = KF = , as shown in figure 7.

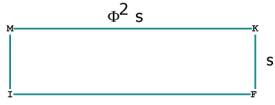
Figure 7 -- showing vertices of the rectangle MKIF.

There are 30 sides to the dodec, and therefore 15 different rectangles.

All of this as explanation of finding the distance OH from Figure 5! Because we are not using trigonometry, we need OH in order to get the pyramid height, OU in Figure 5. Notice that MHFZ is also a rectangle and that HZ is the diagonal of it. If we can find HZ, then OH is just 1/2 of that.
d² = HZ² = MZ² + HM² =
diameter = HZ =

Now we can find OU, the height of the pyramid.
From Area of Pentagon we know the distance mid-face to any vertex of a pentagon =
So UH =

The volume of 1 pyramid = 1/3 * area base * pyramid height =

Note that (from Figure 5) OU / UX = .

What is the surface area of the dodecahedron? It is
12 faces * area of face = , or

What is the central angle of the dodecahedron?
From Figure 5, this is (for example) HOC:

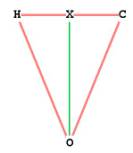
Figure 8 -- dodecahedron central angle
HC = side of dodecahedron, so XH = (1/2)s.

OH = radius = one half HZ = .
sin( XOH) = XH / OH =
XOH = = 20.90515744°
HOC = central angle = 41.81031488°
Since each face of the dodecahedron is a pentagon, the surface angle = 108°

While we're at it, lets get OX, the distance from the centroid to any mid- edge.

OX =

What is the dihedral angle of the dodecahedron?

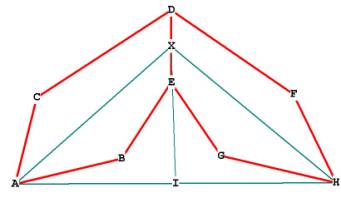
Figure 9

The dihedral angle is AXH. AH is one of the long sides of any of the 15 rectangles which compose the dodec. AX and HX are the height h of the pentagon.
We know from Construction of the Pentagon Part 2 that the height h of the pentagon is:
We know from Figure 7 that AH is , so IH =
sin( IXH) = IH / XH =
We recognize this ratio as our old friend the Phi Triangle with sides in ratio of
IHX = = 58.28252558°.
Dihedral angle AXH = 2 * IXH,
So dihedral angle AXH = 116.5650512°.

Let's compare distances:
Distance from centroid to mid-face (h) = = 1.113516365s.
Distance from centroid to mid-edge = = 1.309016995.
Distance from centroid to vertex = = 1.401258539.

Go back to Figure 6. We have colored the 4 internal pentagonal planes of the dodecahedron. U,X, W and V are the centers of these 4 planes which line up with the centroid O.
What is the distance UX = WV? What is XW?
If we can find these out we can figure out more deeply how the dodecahedron is constructed.

Figure 6, repeated

In Figure 6 we can see that UH on the top plane is the distance from the pentagon center to a vertex.
On plane ADMQK, XM is parallel to UH and is also the distance from that pentagon center to a vertex. UH is connected to XM by HM, a side of the pentagon face CDIMH.
So we have a quadrilateral UHMX, with UH parallel to XM. From here we can derive UX, the distance between the two planes.

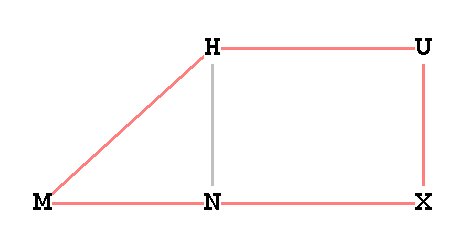
Figure 10 -- dodecahedron planar distance.

We know from Construction of the Pentagon Part 2 that the distance from the center of pentagon to a vertex =
Therefore UH =
The side of the large pentagon ADMQK in Figure 6 is, as we have seen, a diagonal of a dodecahedron face and so the side of the large pentagon = Therefore, XM =
Therefore, XM = *UH, and XM is divided in Mean and Extreme Ratio at N (See Figure 10).
=
HM = s. Triangle MNH is right by construction.
So =
HN =

Notice: UH = UX. So the dodecahedron is designed such that the distance to the 2 large pentagonal planes from the top or bottom faces is exactly equal to the distance between the center and a vertex of any of the faces of the dodecahedron.
This relationship is precisely what we saw in the icosahedron! That makes sense because the two are duals of each other.

The difference is that the dodecahedron is entirely pentagonal, both internally, and externally, on its faces.

What is the distance XW between the 2 large pentagonal planes ADMQK and FEIRP?
Figure 6 is misleading, it looks like the distance must be MI or KF, the dodecahedron side, but it isn't.
We already have enough information to establish this distance.
UX = VW. UV = 2*height of any pyramid =
So XW = UV - 2*UX =
XW =

Notice UX / XW = .
UW is divided in Mean and Extreme Ratio at X.
XV / WV = . XV is divided in Mean and Extreme Ratio at W.

Let's make a chart of these planar distances along the diameter of the dodecahedron as we did with the icosahedron: (see Figure 6):

Relative Chart of Distances –– Pentagonal Planes of Dodecahedron
Relative to the side of the dodecahedron

(Available in the book)

Here is a table of these relationships, letting UX = 1:

(Available in the book)

Note that the diameter of the enclosing sphere is HZ, not UV.
We already know that the diameter is, from page 92,
So what is the distance from U to the top of the sphere, and from V to the bottom of the sphere? Let T’ be the top of the sphere and B’ be the bottom of the sphere. Refer to Figure 6.
If the radius is and the distance OU is , then
UT’ =VB’ =

Finally, let us demonstrate how the dodecahedron may be constructed from the interlocking vertices of 5 tetrahedron. We have already seen how the cube fits inside the dodecahedron, and how 2 interlocking tetrahedron may be formed from the diagonals of the cube. As Buckminster Fuller has pointed out, however, the cube and the dodecahedron are structurally unsound unless bolstered by the additional struts supplied by the tetrahedron. Fuller concludes logically that the tetrahedron is the basic building block of Universe; yet it is the dodecahedron that provides the blueprint and forms the structure for the interlocking tetrahedrons. The dodecahedron unites the geometry of crystals and lattices (root 2 and root 3) with the geometry of Phi (root 5), found in the biology of organic life.

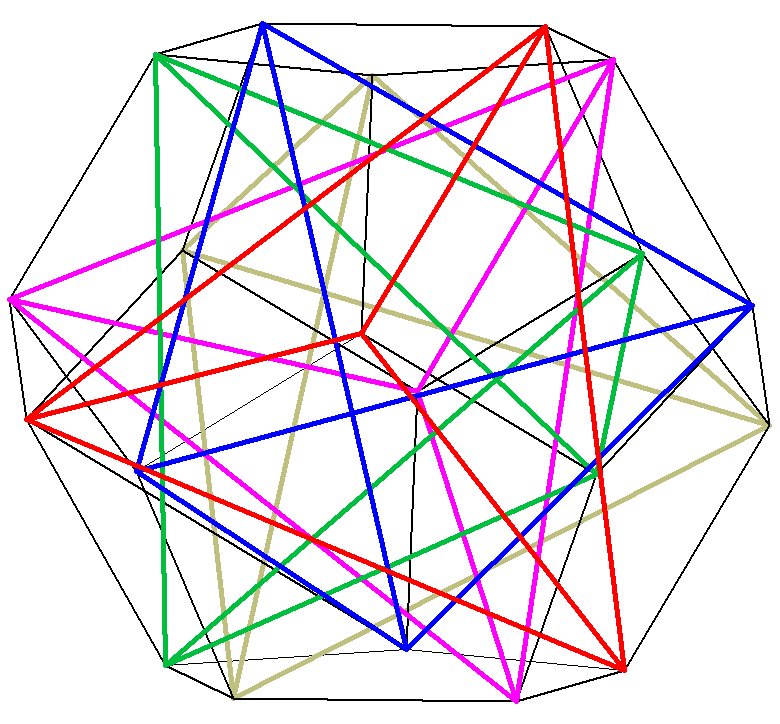
Conclusions:

The dodecahedron is entirely pentagonal, consisting of the geometry of Phi. Yet it contains the and geometry of the cube, tetrahedron, and octahedron.
Remarkably, the sides of the cube are * side of the dodecahedron, because the cube side is the diagonal of a pentagonal face. Here is the key to the relationship of the first three Regular Solids and the much more complex icosahedron and dodecahedron.

Later on in this book we will discover a remarkable polyhedron that defines the relationship and provides the proper nesting for all 5 Platonic Solids, including the icosahedron, directly on its vertices. If a polyhedron could be called exciting, this one is IT! If you can’t wait, go to the last chapter of the book.

Dodecahedron Reference Tables
(included in the book)

Return to Geometry Home Page The Big Picture Home