The nested Platonic Solids can be elegantly represented in the Rhombic
Triacontahedron, as shown in Rhombic
Triacontahedron.
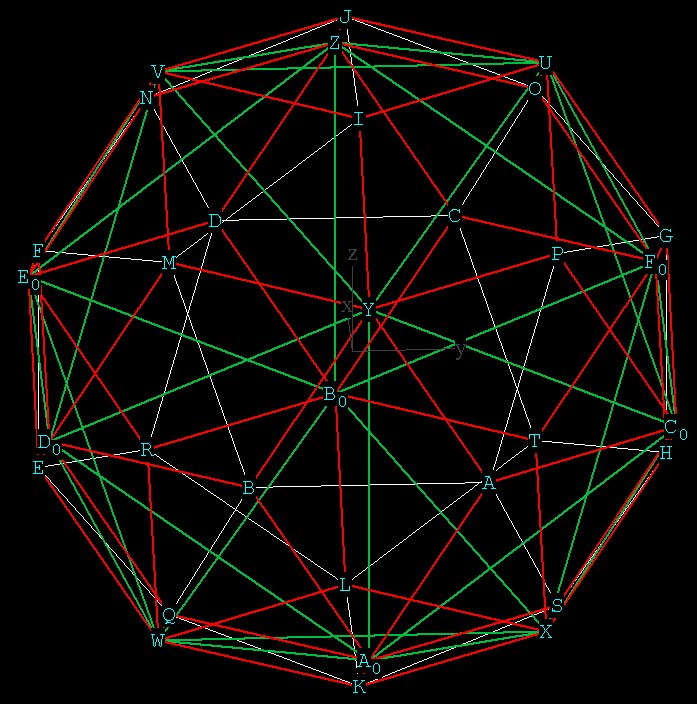
Figure 1 -- the Rhombic Triacontahedron in red with its Phi Ratio
rhombi, the Icosahedron in green with its equilateral triangle faces,
and the Dodecahedron in white with its pentagonal faces. The Rhombic
Triacontahedron is itself a combination of the Icosahedron and the
Dodecahedron, and it demonstrates the proper relationship between the 5
nested Platonic Solids.
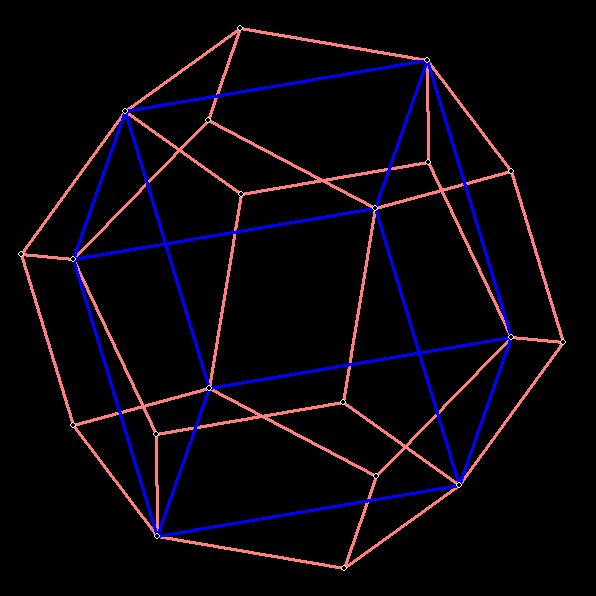
Figure 2 --
The cube fits quite nicely within the dodecahedron, as shown above. The
cube has 8 vertices and 5 different cubes will fit within the
dodecahedron. Each cube has 12 edges, and each edge will be a diagonal
of one of the 12 pentagonal faces of the dodecahedron. Since there are
only 5 diagonals to a pentagon, there can only be 5 different cubes,
each of which will be angled 36 degrees from each other.
(Why is this? Because the diagonals of the pentagon are angled 36 degrees from
each other)
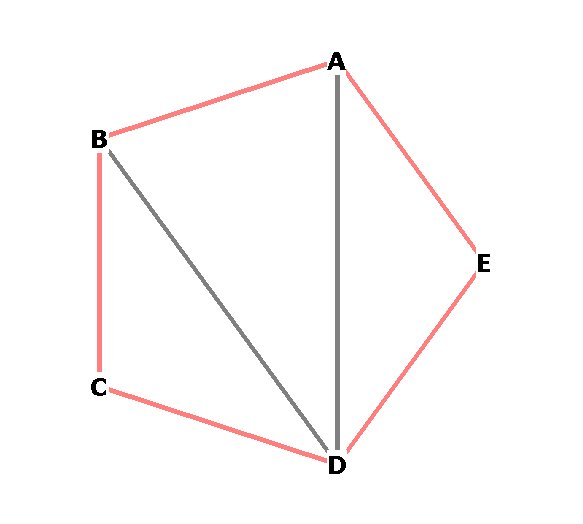
Figure 3 --
Angle BDA is 36 degrees. Triangle BDA is a 36-72-72 golden triangle
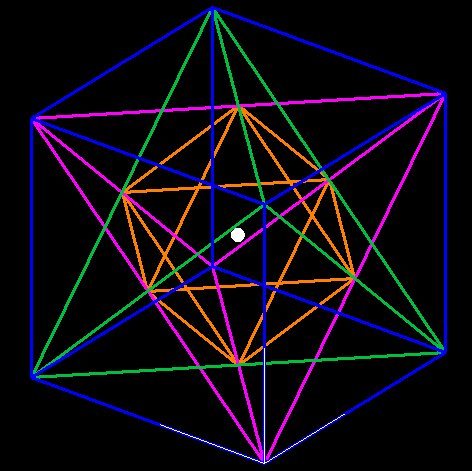
Figure 4 --
The tetrahedron and the octahedron fit nicely within the cube, as shown
above
So the Platonic Solid nesting order as given by the Rhombic
Triacontahedron goes as follows: Icosahedron, Dodecahedron, Cube,
Tetrahedron, Octahedron. Here's how the whole thing looks, all enclosed
within a sphere:
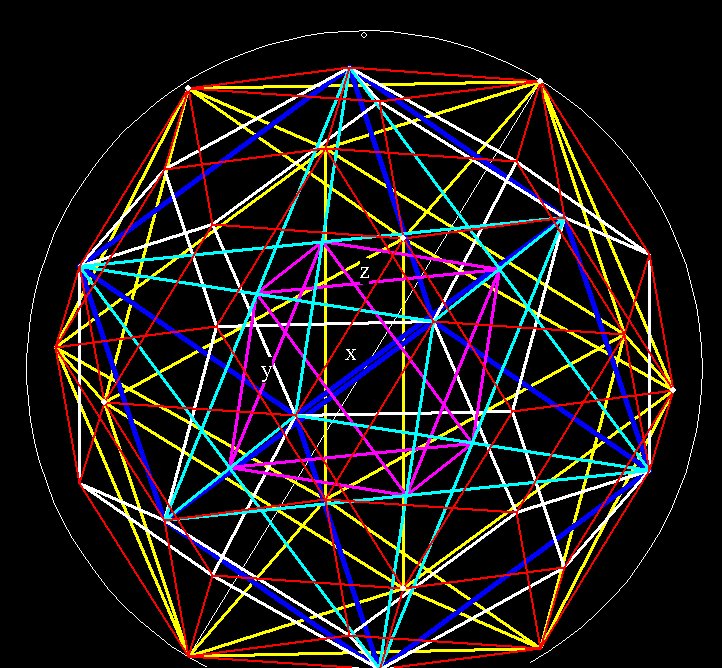
Figure 5 --
The 5 nested Platonic Solids inside a sphere. The Icosahedron in cream,
the rhombic triacontahedron in red, the dodecahedron in white, the cube
in blue, 2 interlocking tetrahedra in cyan, and the octahedron in
magenta. Only the 12 vertices of the icosahedron touch the sphere
boundary.
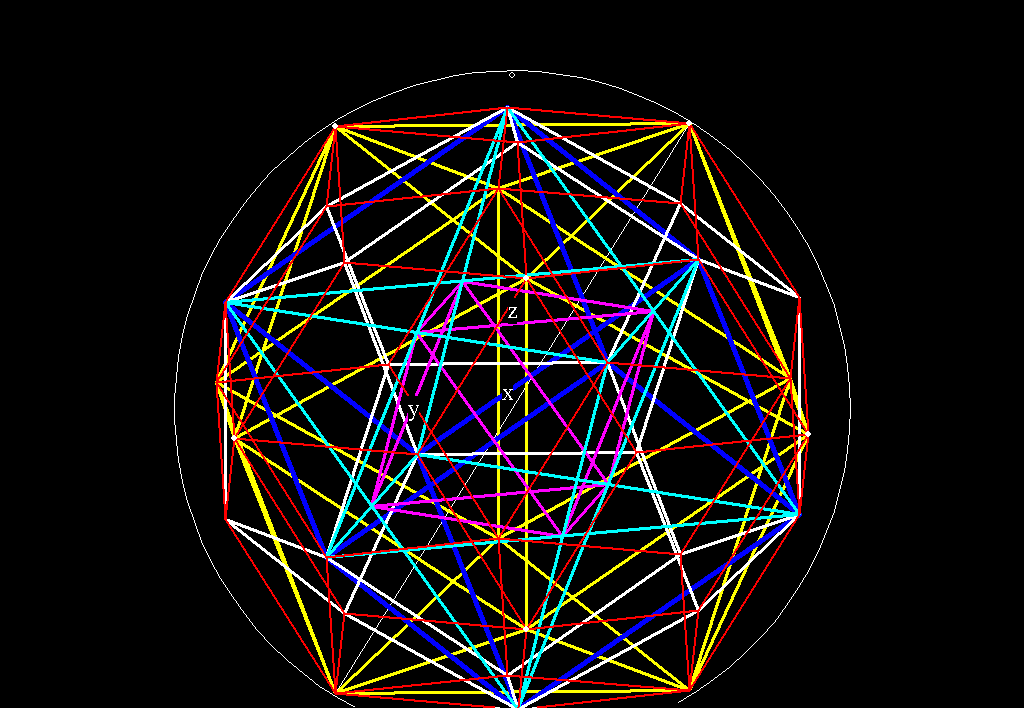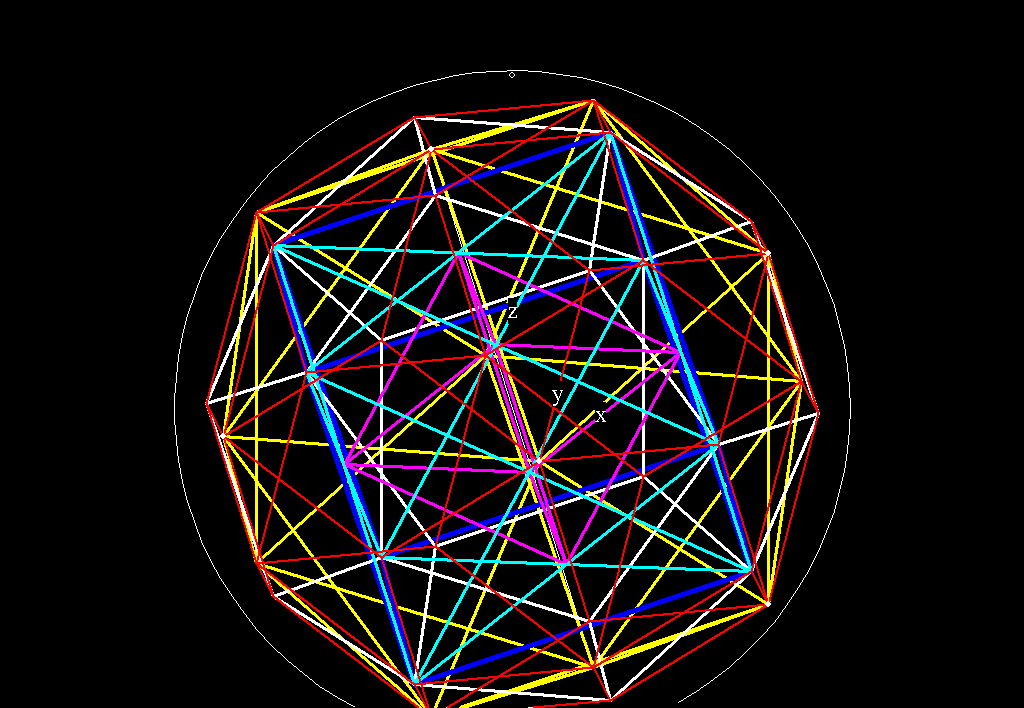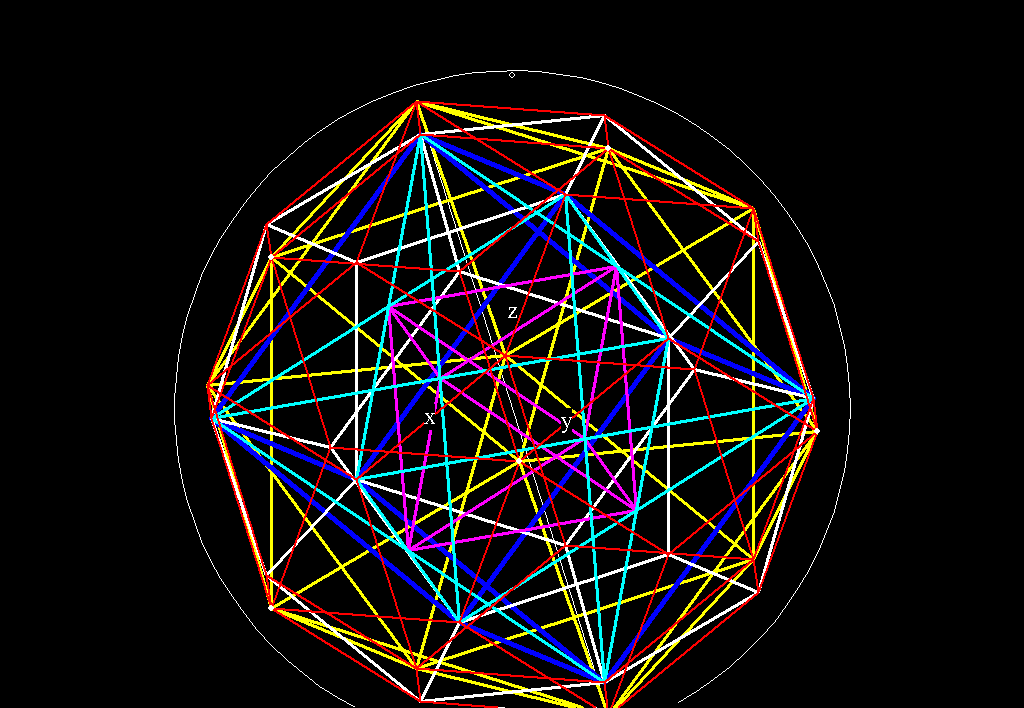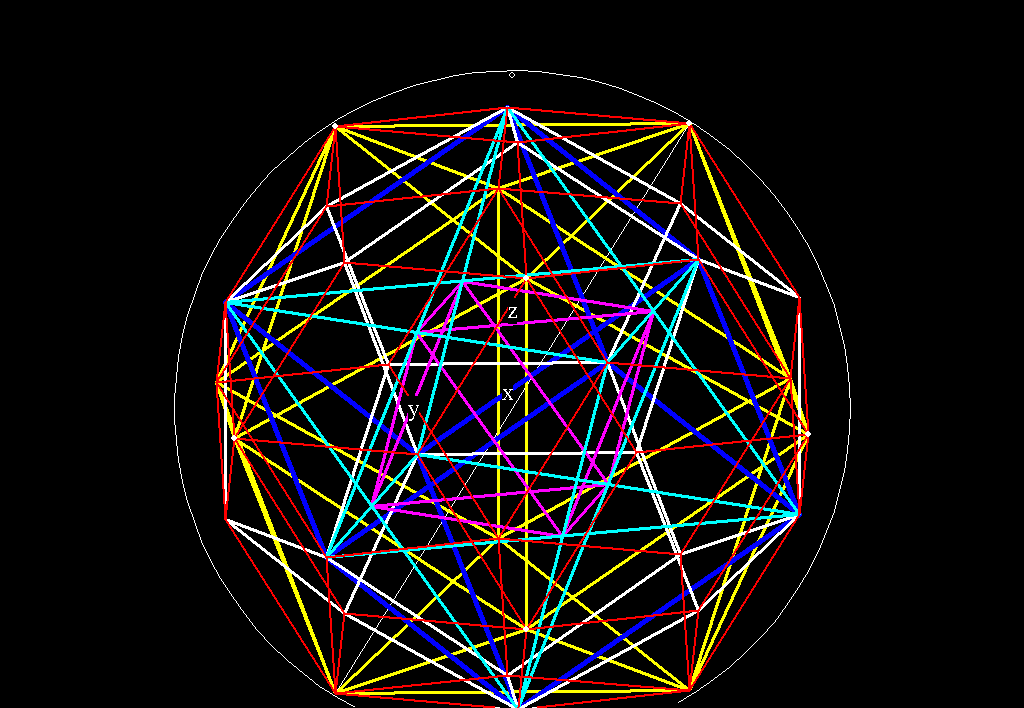
Figure 5A -- Figure 5 as an animated GIF. This is 2.7 Meg file, but
I've included it for those of you with fast download speeds. It's much
easier to distinguish the 5 polyhedra as an animation.
Surprisingly, even though there are 5 Platonic solids, there are only 3
different spheres which contain them. That is because the 4 vertices of
each tetrahedron are 4 of the 8 cube vertices, and the 8 vertices of
the cube are 8 of the 12 vertices of the dodecahedron.
Figure 4 shows that the octahedron is formed from the intersecting
lines of the 2 interlocking tetrahedrons. The edges of the tetrahedrons
are just the diagonals of the cube faces, and the intersection of the
two tetrahedron edges meet precisely at the midpoint of the cube face
(the centroid). If you look at Figure 3 you'll see how the green and
purple lines intersect precisely in the middle of the cube face, making
an "X."
If we let the radius of the sphere which encloses the octahedron = 1,
then what is the radius of the other two spheres?
Since the octahedron is formed from the midpoints of all of the cube
faces, the sphere which encloses it fits precisely within the cube,
like so:
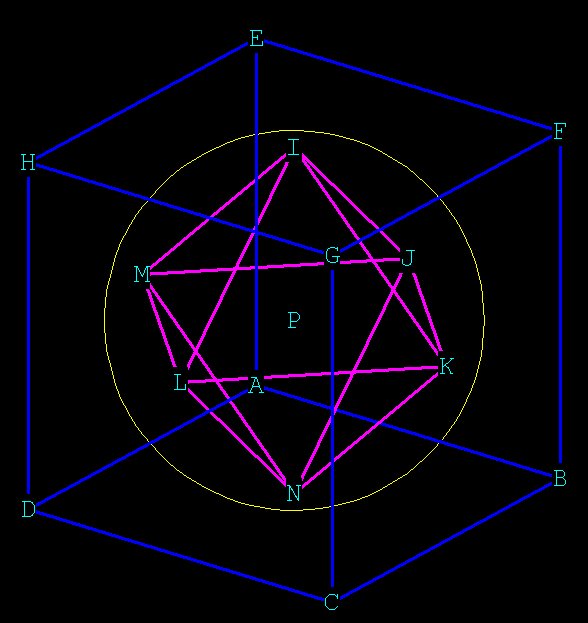
Figure 6 --
The radius of the circle which encloses the octahedron we will
arbitrarily set = 1.
One sphere encloses both the cube and the dodecahedron:
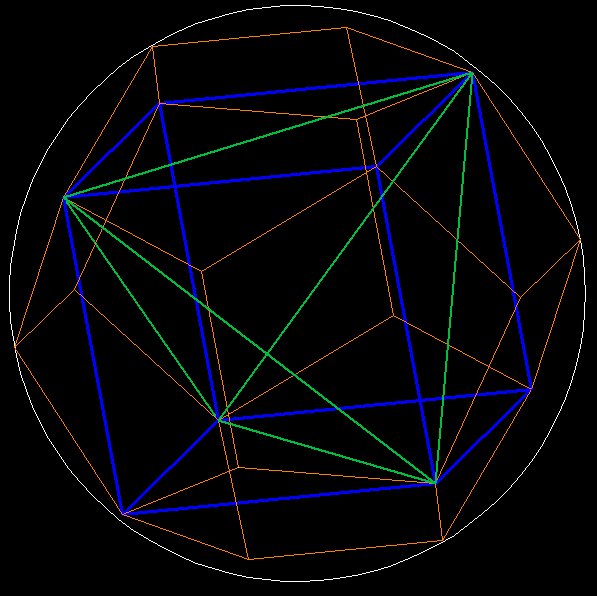
Figure 7 --
The sphere which encloses both dodecahedron and cube.
The radius of this sphere is \/¯ 3 times the sphere which
encloses the octahedron.
The two spheres are the in-sphere of the cube and the circumsphere of
the cube.
The outer sphere which encloses the icosahedron is slightly larger;
\/¯(ز + 1) / \/¯3 larger,
in fact!
So the radii of the three enclosing spheres is: 1,
\/¯3, \/¯(ز
+ 1).
Special characters:
\/¯ ° ¹ ² ³ × ½
¼
Ø \/¯(ز + 1)







