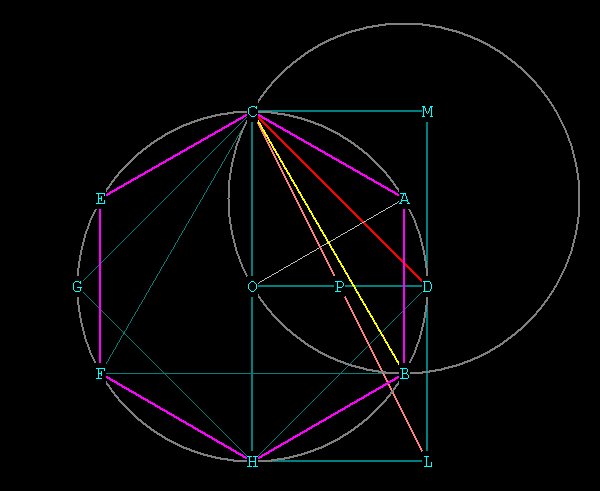This paper will attempt to describe, geometrically,  the precise translation between \/¯5 geometry and it's counterparts, \/¯2 and \/¯3 geometry. I believe this idea has important implications for the design of life forms.
I will explain my ideas as I discovered them, not as a finished product:

Figure 0 -- one of the 30 pyramids of the rhombic triacontahedron. The face of the rhombic triacontahedron.is in red, and the centroid is marked O'.
...........................

While figuring out the central angle IO'J of the rhombic triacontahedron (see Figure 0), I came up with the value for O'I of [\/¯(Ø^4 + 1) / 2] * side dodecahedron.
Note that from  Dodecahedron , that same distance OI = OJ
is calculated to be [\/¯3Ø  / 2] * side dodecahedron.

This  looks wrong.  There's no way that anything related to the \/¯3 can ever be exactly equal to anything with the \/¯5 in it! \/¯3 geometry is the geometry of minerals, crystals, snowflakes, etc.
\/¯5 geometry relates to pentagonally based biological life. Mathematically, the  \/¯3 and the  \/¯5 are entirely different animals.
Here is a  diagram that show this geometrically:

Figure 1 --   \/¯3 and \/¯5 geometry superposed, surrounded by the unit circle (blue).
All of the orange lines belong to the hexagon ( \/¯3).
The large hexagon AQRSTU has sides = r = 1.
The inner hexagon VWYZAoX all have sides =  1 / \/¯3.
The smallest hexagon BoDoEoFoGoCo have sides = (1 / \/¯3) * VWYZAoX = 1/ 3.
And so on. Each smaller hexagon within the pattern has sides (1 / \/¯3) * next larger hexagon.
Notice that the diagonals of the hexagons all intersect at P, the origin.
The green lines belong to the pentagon, which is \/¯5 geometry. We know from  Pentagon Overview that each sucessive inner pentagon has sides = (1 / Ø) * next largest pentagon.
Notice that the orange lines of the pentagon NEVER touch the origin. The pentagon spirals inward, coming ever closer to, but never reaching, the center. It is as if the pentagon is striving mightily for something it can never attain, just as nature attempts to mimic, with the Fibonacci Sequence, the perfect division in Mean and Extreme Ratio.
Notice that NONE of the points of any of the hexagons are common to ANY of the points of any of the pentagons.
 

But it  turns out that                \/¯(Ø^4 + 1) = \/¯3Ø .
And so                          :        \/¯(Ø^4 + 1)  / Ø  =  \/¯3!

Somehow, Ø is able to transform itself into the \/¯3.  When I first made this discovery I was utterly astonished. I always thought the \/¯5 was completely unrelated to the \/¯3, as I show in this diagram:

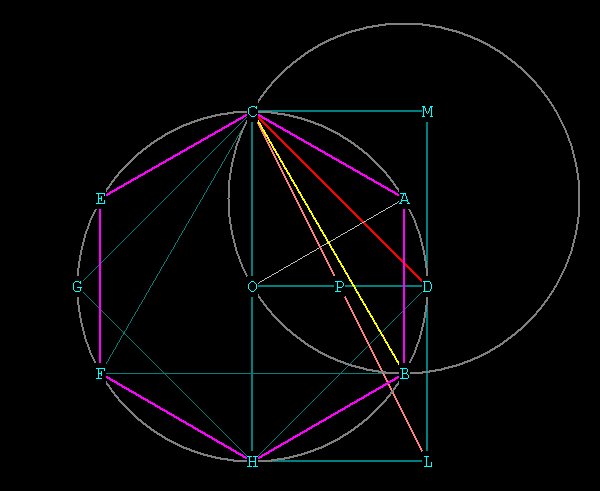
Figure 2  -- showing \/¯2 (CD, red),  \/¯3 (CB, yellow), \/¯5 (CL, orange, L out in left field somewhere).

The \/¯2 is easily explainable, being merely the line between 2 points
separated by 90° on a circle (C and D, the end of the x and y axes, respectively).
The \/¯3 is even more easily explainable, shown by simply connecting 2 points of a hexagon, or by connecting the intersecting points of a circle (CB).
The \/¯5 requires the double square CMLH, and the point L is at a strange position.
Or is it??

Take a look at this:

Figure 3  -- determination of the point L.

AO = BH, being the radial distance of  circles at O,A and B.
BJ is an extension of AB, the side of the hexagon.
BI = BJ.
ID = JL.
Triangle  AOI congruent to triangle BHJ .
Triangle AID congruent to triangle BLJ.
OD = HL  = r.
AI = BJ = 1/2 * r.
OI = HJ.
HJ² = BH² - BJ²  =   r² - 1/4 r² = 3/4 r².
HJ =   (\/¯3 / 2)r.
JL = HL - HJ =  r -  (\/¯3 / 2)r.  =  [(2 -  \/¯3)  / 2]r.

So from Figure 3 it looks like point L, on the  \/¯5 line CL, is on a line tangent to the circle with center at  O, (the line ML) and that it's distance from the side of the hexagon (AB) is the same as for the  \/¯2 diagonal (CD) of the square CMDO. This distance involves the  \/¯3 (see JL above).  This is looking interesting, maybe there's a geometric connection between  \/¯3 and  \/¯5 after all.

Figure 4  --- Showing that Point L is actually easily explainable -- being merely the endpoint of the vesica (intersection) along the x axis (HR) of the 2 circles at H and at R

So we were right -- L is tangent to the unit circle centered at H

But what is the relation geometrically between  \/¯Ø^4 + 1,   \/¯3, and Ø?
How would  \/¯(Ø^4 + 1) /  Ø   transform into the  \/¯3?

Ultimately we are looking for the geometric relationship between  Ø and  \/¯3.
Amazingly enough, there is a relationship: ز  + (1 / ز)  = 3.
Try it on your calculator.  Ø = 1.618033989, or, more accurately, (1 +  \/¯5)  / 2.
This equation can be considered geometrically  as a  Ø,  1 / Ø, \/¯3  (right) triangle.
The angles are:      90°, 20.90515742°, 69.09484258°.

Here is a diagram:

Figure 5 -- showing the geometric relationship between Ø  and the  \/¯3, specifically,
the  Ø to \/¯3 conversion triangle.
The purple lines (hexagon) = r = \/¯1.
The red line (square diagonal) = \/¯2.
The yellow line (large vesica diagonal) = \/¯3.
AD =  \/¯4.
The orange line ( double square diagonal) = \/¯5.
The  Ø to \/¯3 conversion triangle is in blue.

The triangle AGL (in blue) is the geometry of the relationship between  \/¯3 and Ø .
AG = 1 / Ø.
GL = Ø.
AL =  \/¯3.
I have drawn the large circle with centerA (in cream), which passes through the endpoints of the large vesica's at R, E, and C. The circle represents all points with the distance \/¯3 from A.

The triangle says:
ز  + (1 / ز)  = 3,     (Ø^4  + 1) / ز  = 3,  taking square roots we get
\/¯(Ø^4 + 1)  / Ø  =  \/¯3, which is where we started.

Figure 6 showing how to construct the conversion triangle and its relationship to the pentagon.

Here we see that in order to determine the Ø to  \/¯3 conversion triangle, we must get the point G. G can be determined simply by a construction of the pentagon (see  Construction Of The Pentagon ).

Fo = G  is determined from ABo, which is  \/¯5.
When one-half that distance (AEo) is transferred to the horizontal (x axis, line ZY), we get EoFo. OFo is now  (\/¯5 / 2)  - (1 / 2) = 1 / Ø = 0.618033989.
By finding OFo, one can draw a line from Fo parallel to OA to find G, the short leg of the conversion triangle. OFo = AG = 1 / Ø.  FoG = OA = 1, the radius of the unit circle centered at O and going through A.
The distance GL can easily be determined WITHOUT  the '\/¯3 circle'. All that is necessary to do is draw a perpendicular from Fo to hit AN at G, and then notice that FoG = AO = 1. Then add to FoG the distance AG to find L. Now we have all 3 points of the triangle, and AL can be connected to give the \/¯3.
(Remember that 1 + (1 / Ø) = Ø).
During the construction of the pentagon, the distance OFo is determined which is the short leg of the conversion triangle. AFo is the side of the pentagon AGo. I have drawn a blue circle to indicate this distance, which is also the side of the pentagon AHo.
It is clear from the geometry that the  \/¯3 can be determined from  Ø, and not vice-versa.
Therefore, the \/¯3  results from the division in Extreme and Mean Ratio, which is  Ø!

The implications of this are enormous, in my mind. It means that the imprecise, ever-striving-for-perfection, dynamic-tensional construction of biologically based life, based upon the pentagon, is a bridge to minerals, rocks, crystals, snowflakes, etc., which are based upon the perfection of \/¯3 geometry.

The dodecahedron contains within it this conversion triangle! Recall from  Dodecahedron  that the dodec is composed of 15   1,  ز rectangles and therefore 30   1, ز,  \/¯3Ø triangles!

The corners of the dodecahedron can be made from ز,1 rectangles (meaning if the short side is 1, the long side is ز in relation to it).

Fig 7 -- Showing the  Ø to \/¯3  conversion triangle within the dodecahedron.
The conversion triangle is either  MHO or FOH.

The following remarkable fact emerges: by the Pythagorean Theorem, the diagonal of this ز rectangle is \/¯(Ø^4 + 1). But \/¯(Ø^4 + 1) = \/¯3 * Ø!
Or, \/¯(Ø^4 + 1) / Ø = \/¯3.
This triangle is similar to the Ø, 1 / Ø, \/¯3 conversion triangle in Figure 8C because if we divide the long side of the conversion triangle in Figure 8C and do the same for the ز , 1 triangle in the dodecahedron, we get:
                Ø / (1 / Ø)  = ز  and
                ز / 1         = ز   .
The dodecahedron contains, as part of its structure, the code to convert between \/¯3 and \/¯5 geometry.
So the dodecahedron is the blueprint, geometrically, for the conversion of biologically based life forms  to crystalline life forms.

There is also a conversion triangle between Ø and the \/¯2.
This triangle is a  (1 / Ø),  \/¯Ø,   \/¯2 right triangle. This can be shown by the equation
(1 / Ø)² +  (\/¯Ø)²  =   (\/¯2)²,   or,  1 / ز  + Ø   =  2.
Geometrically, we can see this as follows:

Figure 8 -- showing also the Ø to  \/¯2 conversion triangle, in red.
The short leg is 1 / Ø, the long leg is \/¯Ø, the hypotenuse is \/¯2.

Now we have a direct geometric link between the geometry of crystals, minerals, etc and biological life. Most of these life forms are designed in a lattice structure which is cubic or hexagonal. This is
\/¯2 and \/¯3 geometry. Of course the hexagonal structure is also found in organic compounds (benzene ring) and even in human DNA, along with the pentagon, as shown in Figure 9. This paper may shed some light, geometrically, how the two life forms are related.

Figure 9 -- 1 The nucleotide, an integral component of human DNA  ***

Of course,  Ø has the fascinating property that multiples of it can be combined to form any integer. here is a brief table:
1     =   1 / Ø + 1 / ز
2     =   Ø  +  1 / ز
3     =   ز  + 1 / ز
4     =   ز  + 1 + 1 / ز   or    س   -  1 / س
5     =   س  +  1 / Ø  +  1 / Ø^4
6     =   multiple of 2, 3
7     =   Ø^4 +  1 / Ø^4
8     =   multiple of 2,4
9     =   multiple of 3
10   =   multiple of 2 , 5
11   =   Ø^4 + ز + 1 + 1 / ز + 1 / Ø^4  or    Ø^4 + ز + 4 / ز
12   =   multiple of 2, 3, 4
13   =   Ø^5 + Ø + (2 / Ø^4 )
*
*
*
etc
This is a fascinating property of  the division in Mean and Extreme Ratio, based upon the \/¯5 .
Ø is an irrational number but in it's relationship with itself, can form whole numbers.
Perhaps this is true of other numbers as well, but we have seen geometrically in these papers that Ø
is an integral part of many polyhedra, and there are many sources which show the division in Mean and Extreme Ratio is used extensively in nature  to construct life forms.
 
 

Speculation:
As we saw in  2 Dimensional Geometry  and  3 Dimensional Geometry , the hexagon / interlocking tetrahedron, and equilateral triangle / tetrahedron  are the first figures which can be constructed. The square / cube follows from that.  This geometry leads to a perfect universe of harmony, where everything can be predicted and everything is known. This geometry can spread out infinitely large, or shrink infinitely small. The origin or center of this geometry is known from the very beginning, and any time we want we can go to origin point and back out the other side. But such a geometry is static, non-changing. There is no dynamic tension within it. It is perfectly stable, but there is no excitement. If you take a look at electron micoscope pics of minerals and crystals, you see this perfect matrix of atomic structure.
A great web site to observe this is at:  <http://www.kings.edu/~chemlab/vrml/index.html>.
Division in Extreme and Mean Ratio is, on the other hand,  also a perfect, harmonious  division with absolutely not the most infinitely small particle left over to cause 'noise', but this division is impossible to attain in the physical universe, because it has no origin point, no starting point! It has to be approximated in nature by the Fibonacci Sequence.
But life based upon the division in Extreme and Mean Ratio is dynamic, unpredictable, and exciting. Pentagonally based life can never attain the perfection it is conceptually based upon, but it constantly strives to do so. It is always searching for it's origins, for the truth about itself.  This is the basic impulse, geometrically, of creativity.
Pentagonally based life can never find the origin, or genesis point, because there IS NO genesis point! That is clear from Figure 1. The pentagons spiral inward, always reaching for, but never attaining, its beginning.
So our conversion triangles state an important relationship mathematically and geometrically, and, I believe, between  2 different life forms that co-exist on planet earth.

On to  Further Explorations of the Conversion Triangle
_____________________________________________________________________
*** Taken from from http://www.dnaftb.org/dnaftb/ Section 15 of  'DNA From the Beginning'.
 

Special characters:
 \/¯ ­ ° ¹ ² ³ × ½ ¼ Ø  \/¯(ز + 1)